Compressing deep neural networks by matrix product operators

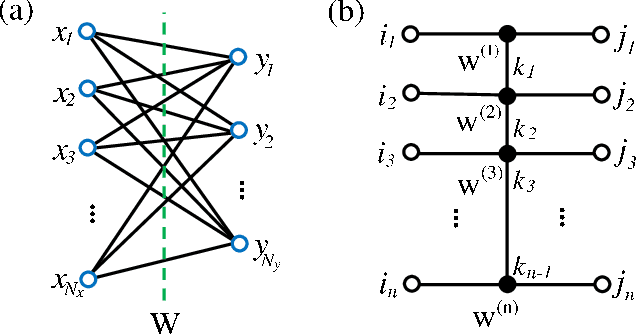
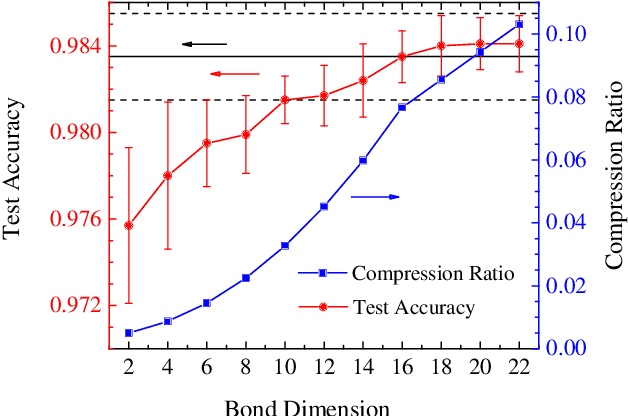
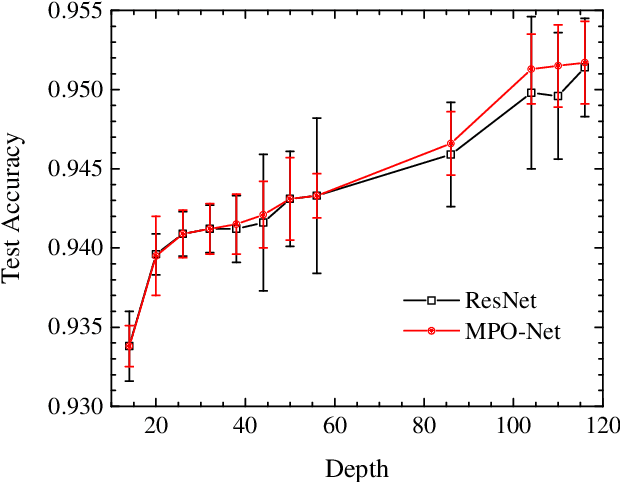
A deep neural network is a parameterization of a multi-layer mapping of signals in terms of many alternatively arranged linear and nonlinear transformations. The linear transformations, which are generally used in the fully-connected as well as convolutional layers, contain most of the variational parameters that are trained and stored. Compressing a deep neural network to reduce its number of variational parameters but not its prediction power is an important but challenging problem towards the establishment of an optimized scheme in training efficiently these parameters and in lowering the risk of overfitting. Here we show that this problem can be effectively solved by representing linear transformations with matrix product operators (MPO). We have tested this approach in five main neural networks, including FC2, LeNet-5, VGG, ResNet, and DenseNet on two widely used datasets, namely MNIST and CIFAR-10, and found that this MPO representation indeed sets up a faithful and efficient mapping between input and output signals, which can keep or even improve the prediction accuracy with dramatically reduced number of parameters.