Hyper Evidential Deep Learning to Quantify Composite Classification Uncertainty

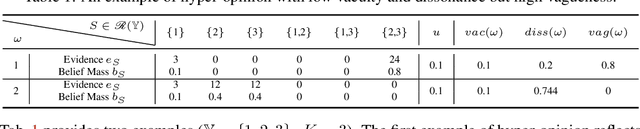
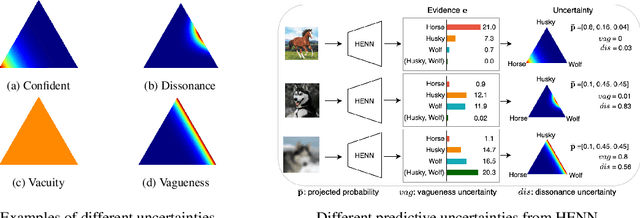
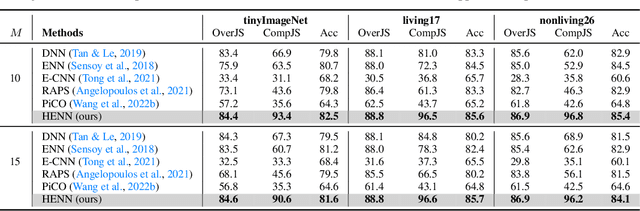
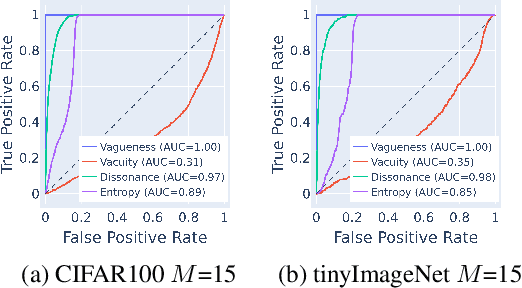
Deep neural networks (DNNs) have been shown to perform well on exclusive, multi-class classification tasks. However, when different classes have similar visual features, it becomes challenging for human annotators to differentiate them. This scenario necessitates the use of composite class labels. In this paper, we propose a novel framework called Hyper-Evidential Neural Network (HENN) that explicitly models predictive uncertainty due to composite class labels in training data in the context of the belief theory called Subjective Logic (SL). By placing a grouped Dirichlet distribution on the class probabilities, we treat predictions of a neural network as parameters of hyper-subjective opinions and learn the network that collects both single and composite evidence leading to these hyper-opinions by a deterministic DNN from data. We introduce a new uncertainty type called vagueness originally designed for hyper-opinions in SL to quantify composite classification uncertainty for DNNs. Our results demonstrate that HENN outperforms its state-of-the-art counterparts based on four image datasets. The code and datasets are available at: https://github.com/Hugo101/HyperEvidentialNN.

Multidimensional Uncertainty-Aware Evidential Neural Networks

Traditional deep neural networks (NNs) have significantly contributed to the state-of-the-art performance in the task of classification under various application domains. However, NNs have not considered inherent uncertainty in data associated with the class probabilities where misclassification under uncertainty may easily introduce high risk in decision making in real-world contexts (e.g., misclassification of objects in roads leads to serious accidents). Unlike Bayesian NN that indirectly infer uncertainty through weight uncertainties, evidential NNs (ENNs) have been recently proposed to explicitly model the uncertainty of class probabilities and use them for classification tasks. An ENN offers the formulation of the predictions of NNs as subjective opinions and learns the function by collecting an amount of evidence that can form the subjective opinions by a deterministic NN from data. However, the ENN is trained as a black box without explicitly considering inherent uncertainty in data with their different root causes, such as vacuity (i.e., uncertainty due to a lack of evidence) or dissonance (i.e., uncertainty due to conflicting evidence). By considering the multidimensional uncertainty, we proposed a novel uncertainty-aware evidential NN called WGAN-ENN (WENN) for solving an out-of-distribution (OOD) detection problem. We took a hybrid approach that combines Wasserstein Generative Adversarial Network (WGAN) with ENNs to jointly train a model with prior knowledge of a certain class, which has high vacuity for OOD samples. Via extensive empirical experiments based on both synthetic and real-world datasets, we demonstrated that the estimation of uncertainty by WENN can significantly help distinguish OOD samples from boundary samples. WENN outperformed in OOD detection when compared with other competitive counterparts.

Quantifying Classification Uncertainty using Regularized Evidential Neural Networks

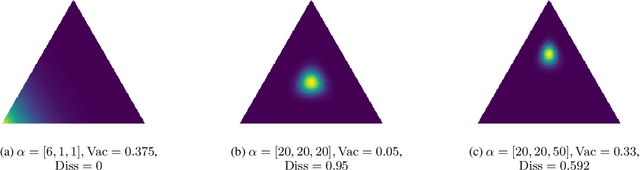
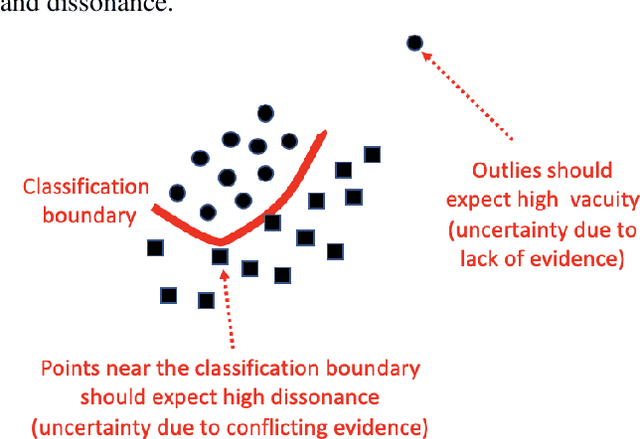
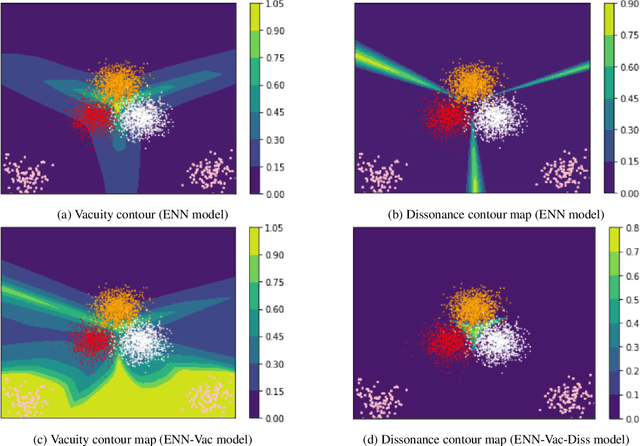
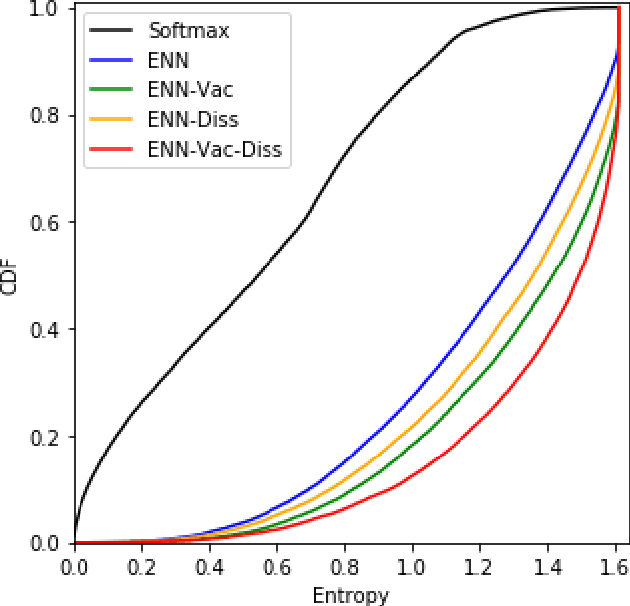
Traditional deep neural nets (NNs) have shown the state-of-the-art performance in the task of classification in various applications. However, NNs have not considered any types of uncertainty associated with the class probabilities to minimize risk due to misclassification under uncertainty in real life. Unlike Bayesian neural nets indirectly infering uncertainty through weight uncertainties, evidential neural networks (ENNs) have been recently proposed to support explicit modeling of the uncertainty of class probabilities. It treats predictions of an NN as subjective opinions and learns the function by collecting the evidence leading to these opinions by a deterministic NN from data. However, an ENN is trained as a black box without explicitly considering different types of inherent data uncertainty, such as vacuity (uncertainty due to a lack of evidence) or dissonance (uncertainty due to conflicting evidence). This paper presents a new approach, called a {\em regularized ENN}, that learns an ENN based on regularizations related to different characteristics of inherent data uncertainty. Via the experiments with both synthetic and real-world datasets, we demonstrate that the proposed regularized ENN can better learn of an ENN modeling different types of uncertainty in the class probabilities for classification tasks.