Teaching Diffusion to Speculate Left-to-Right

Large language models (LLMs) achieve remarkable performance across a wide range of tasks, but their autoregressive decoding process incurs substantial inference costs due to inherently sequential token generation. Speculative decoding addresses this bottleneck by employing a lightweight draft model to propose multiple future tokens that are subsequently verified in parallel by a larger target model. Recent work has demonstrated that diffusion language models are well suited for this setting, as they can generate entire blocks of draft tokens in parallel and thereby alleviate the sequential constraints of autoregressive drafting. A subtlety of this regime is that block-diffusion drafters generate tokens bidirectionally within a block, whereas verification is performed by an autoregressive target model that evaluates tokens in a strictly left-to-right manner, leaving a gap between the symmetric training-time objective and the asymmetric verification-time reward. In this work, we offer an empirical analysis of three training-time interventions that narrow this gap: token positional weighting, a first-error focal loss that targets the position that breaks the accepted prefix within each block, and a chain loss term that substitutes a differentiable surrogate for the expected accepted length. The three interventions act along orthogonal axes (position, block-conditional first error, joint prefix) and compose additively; they are likewise orthogonal to test-time alignment mechanisms such as multi-draft self-selection, with which they can in principle be combined. Across four target models and six reasoning, code, and dialogue benchmarks, the three interventions raise accepted draft length by 21-76% per benchmark over a position-uniform baseline, without adding additional forward passes and without changing the inference pipeline or the rejection-sampling exactness contract.

LibriTTS-VI: A Public Corpus and Novel Methods for Efficient Voice Impression Control

Fine-grained control over voice impressions (e.g., making a voice brighter or calmer) is a key frontier for creating more controllable text-to-speech. However, this nascent field faces two key challenges. The first is the problem of impression leakage, where the synthesized voice is undesirably influenced by the speaker's reference audio, rather than the separately specified target impression, and the second is the lack of a public, annotated corpus. To mitigate impression leakage, we propose two methods: 1) a training strategy that separately uses an utterance for speaker identity and another utterance of the same speaker for target impression, and 2) a novel reference-free model that generates a speaker embedding solely from the target impression, achieving the benefits of improved robustness against the leakage and the convenience of reference-free generation. Objective and subjective evaluations demonstrate a significant improvement in controllability. Our best method reduced the mean squared error of 11-dimensional voice impression vectors from 0.61 to 0.41 objectively and from 1.15 to 0.92 subjectively, while maintaining high fidelity. To foster reproducible research, we introduce LibriTTS-VI, the first public voice impression dataset released with clear annotation standards, built upon the LibriTTS-R corpus.

Scheduled Interleaved Speech-Text Training for Speech-to-Speech Translation with LLMs

Speech-to-speech translation (S2ST) has been advanced with large language models (LLMs), which are fine-tuned on discrete speech units. In such approaches, modality adaptation from text to speech has been an issue. LLMs are trained on text-only data, which presents challenges to adapt them to speech modality with limited speech-to-speech data. To address the training difficulty, we propose scheduled interleaved speech--text training in this study. We use interleaved speech--text units instead of speech units during training, where aligned text tokens are interleaved at the word level. We gradually decrease the ratio of text as training progresses, to facilitate progressive modality adaptation from text to speech. We conduct experimental evaluations by fine-tuning LLaMA3.2-1B for S2ST on the CVSS dataset. We show that the proposed method consistently improves the translation performances, especially for languages with limited training data.

Ensemble ToT of LLMs and Its Application to Automatic Grading System for Supporting Self-Learning

Providing students with detailed and timely grading feedback is essential for self-learning. While existing LLM-based grading systems are promising, most of them rely on one single model, which limits their performance. To address this, we propose Ensemble Tree-of-Thought (ToT), a framework that enhances LLM outputs by integrating multiple models. Using this framework, we develop a grading system. Ensemble ToT follows three steps: (1) analyzing LLM performance, (2) generating candidate answers, and (3) refining them into a final result. Based on this, our grading system first evaluates the grading tendencies of LLMs, then generates multiple results, and finally integrates them via a simulated debate. Experimental results demonstrate our approach's ability to provide accurate and explainable grading by effectively coordinating multiple LLMs.

Polynomial time constructive decision algorithm for multivariable quantum signal processing

Quantum signal processing (QSP) and quantum singular value transformation (QSVT) have provided a unified framework for understanding many quantum algorithms, including factorization, matrix inversion, and Hamiltonian simulation. As a multivariable version of QSP, multivariable quantum signal processing (M-QSP) is proposed. M-QSP interleaves signal operators corresponding to each variable with signal processing operators, which provides an efficient means to perform multivariable polynomial transformations. However, the necessary and sufficient condition for what types of polynomials can be constructed by M-QSP is unknown. In this paper, we propose a classical algorithm to determine whether a given pair of multivariable Laurent polynomials can be implemented by M-QSP, which returns True or False. As one of the most important properties of this algorithm, it returning True is the necessary and sufficient condition. The proposed classical algorithm runs in polynomial time in the number of variables and signal operators. Our algorithm also provides a constructive method to select the necessary parameters for implementing M-QSP. These findings offer valuable insights for identifying practical applications of M-QSP.

Head-Related Transfer Function Interpolation from Spatially Sparse Measurements Using Autoencoder with Source Position Conditioning

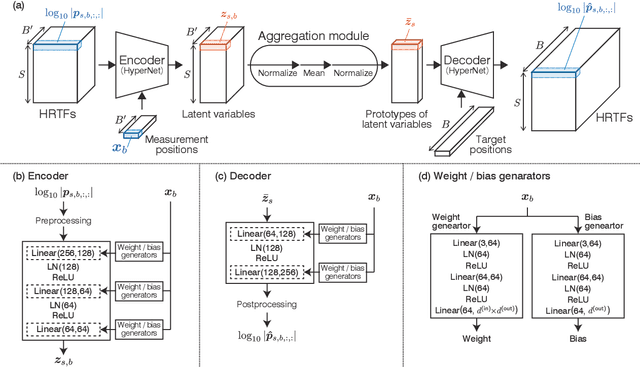
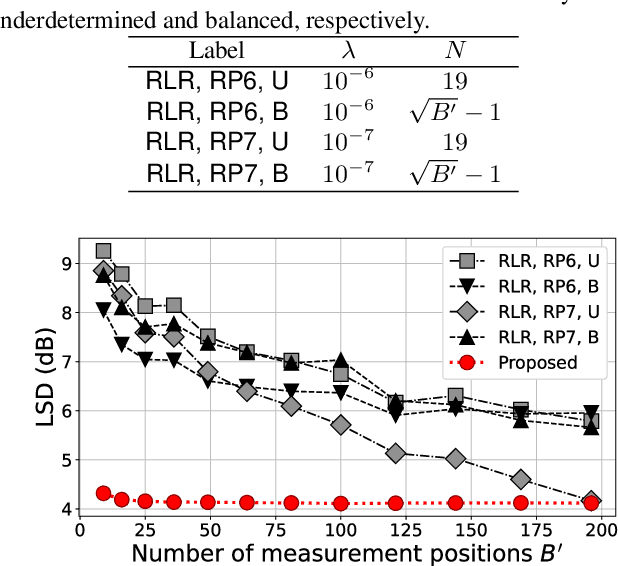
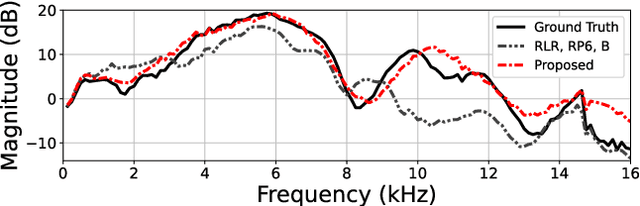
We propose a method of head-related transfer function (HRTF) interpolation from sparsely measured HRTFs using an autoencoder with source position conditioning. The proposed method is drawn from an analogy between an HRTF interpolation method based on regularized linear regression (RLR) and an autoencoder. Through this analogy, we found the key feature of the RLR-based method that HRTFs are decomposed into source-position-dependent and source-position-independent factors. On the basis of this finding, we design the encoder and decoder so that their weights and biases are generated from source positions. Furthermore, we introduce an aggregation module that reduces the dependence of latent variables on source position for obtaining a source-position-independent representation of each subject. Numerical experiments show that the proposed method can work well for unseen subjects and achieve an interpolation performance with only one-eighth measurements comparable to that of the RLR-based method.

Profiling based Out-of-core Hybrid Method for Large Neural Networks

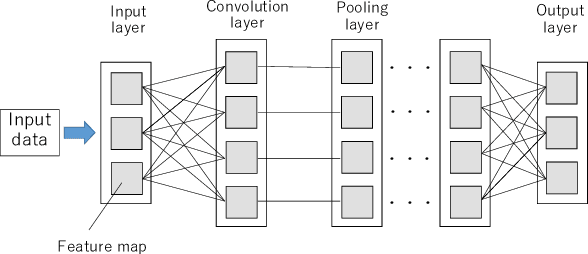
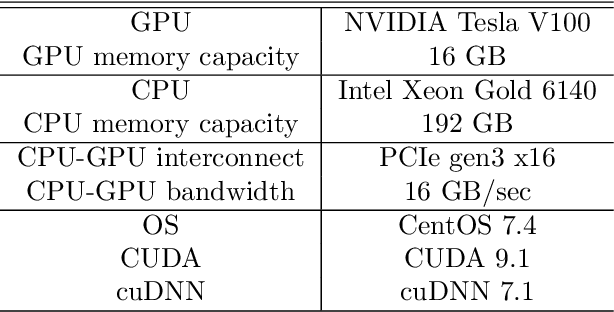
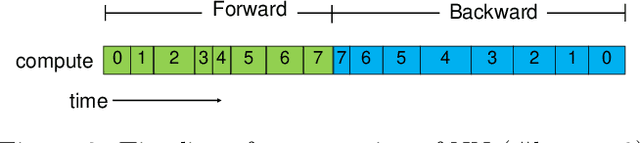
GPUs are widely used to accelerate deep learning with NNs (NNs). On the other hand, since GPU memory capacity is limited, it is difficult to implement efficient programs that compute large NNs on GPU. To compute NNs exceeding GPU memory capacity, data-swapping method and recomputing method have been proposed in existing work. However, in these methods, performance overhead occurs due to data movement or increase of computation. In order to reduce the overhead, it is important to consider characteristics of each layer such as sizes and cost for recomputation. Based on this direction, we proposed Profiling based out-of-core Hybrid method (PoocH). PoocH determines target layers of swapping or recomputing based on runtime profiling. We implemented PoocH by extending a deep learning framework, Chainer, and we evaluated its performance. With PoocH, we successfully computed an NN requiring 50 GB memory on a single GPU with 16 GB memory. Compared with in-core cases, performance degradation was 38 \% on x86 machine and 28 \% on POWER9 machine.