MAGE: A Multi-Agent Engine for Automated RTL Code Generation

The automatic generation of RTL code (e.g., Verilog) through natural language instructions has emerged as a promising direction with the advancement of large language models (LLMs). However, producing RTL code that is both syntactically and functionally correct remains a significant challenge. Existing single-LLM-agent approaches face substantial limitations because they must navigate between various programming languages and handle intricate generation, verification, and modification tasks. To address these challenges, this paper introduces MAGE, the first open-source multi-agent AI system designed for robust and accurate Verilog RTL code generation. We propose a novel high-temperature RTL candidate sampling and debugging system that effectively explores the space of code candidates and significantly improves the quality of the candidates. Furthermore, we design a novel Verilog-state checkpoint checking mechanism that enables early detection of functional errors and delivers precise feedback for targeted fixes, significantly enhancing the functional correctness of the generated RTL code. MAGE achieves a 95.7% rate of syntactic and functional correctness code generation on VerilogEval-Human 2 benchmark, surpassing the state-of-the-art Claude-3.5-sonnet by 23.3 %, demonstrating a robust and reliable approach for AI-driven RTL design workflows.

RA-PbRL: Provably Efficient Risk-Aware Preference-Based Reinforcement Learning

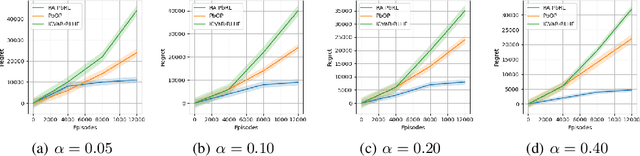
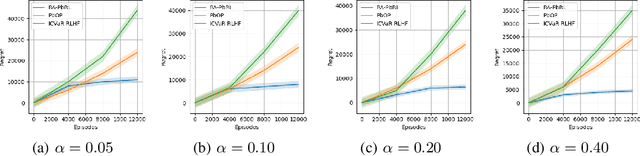
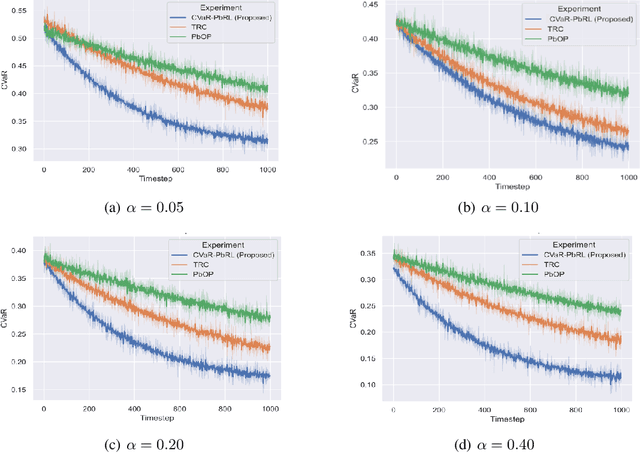
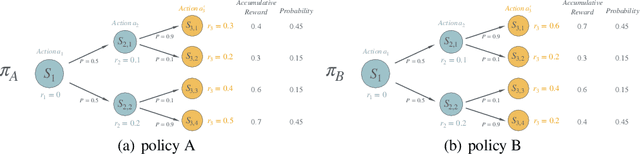
Preference-based Reinforcement Learning (PbRL) studies the problem where agents receive only preferences over pairs of trajectories in each episode. Traditional approaches in this field have predominantly focused on the mean reward or utility criterion. However, in PbRL scenarios demanding heightened risk awareness, such as in AI systems, healthcare, and agriculture, risk-aware measures are requisite. Traditional risk-aware objectives and algorithms are not applicable in such one-episode-reward settings. To address this, we explore and prove the applicability of two risk-aware objectives to PbRL: nested and static quantile risk objectives. We also introduce Risk-Aware- PbRL (RA-PbRL), an algorithm designed to optimize both nested and static objectives. Additionally, we provide a theoretical analysis of the regret upper bounds, demonstrating that they are sublinear with respect to the number of episodes, and present empirical results to support our findings. Our code is available in https://github.com/aguilarjose11/PbRLNeurips.

A Survey of Numerical Algorithms that can Solve the Lasso Problems

In statistics, the least absolute shrinkage and selection operator (Lasso) is a regression method that performs both variable selection and regularization. There is a lot of literature available, discussing the statistical properties of the regression coefficients estimated by the Lasso method. However, there lacks a comprehensive review discussing the algorithms to solve the optimization problem in Lasso. In this review, we summarize five representative algorithms to optimize the objective function in Lasso, including the iterative shrinkage threshold algorithm (ISTA), fast iterative shrinkage-thresholding algorithms (FISTA), coordinate gradient descent algorithm (CGDA), smooth L1 algorithm (SLA), and path following algorithm (PFA). Additionally, we also compare their convergence rate, as well as their potential strengths and weakness.

Three-dimensional instantaneous orbit map for rotor-bearing system based on a novel multivariable complex variational mode decomposition algorithm

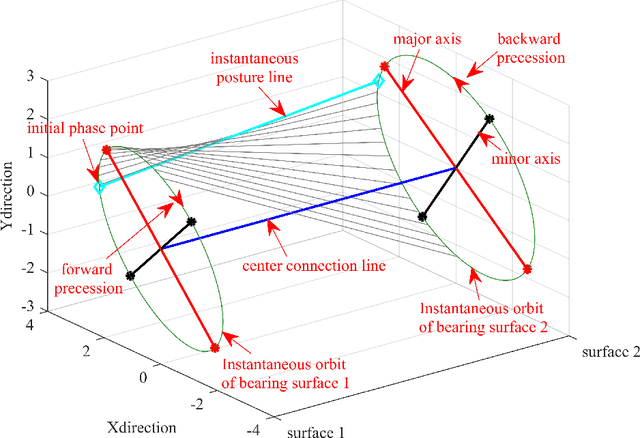
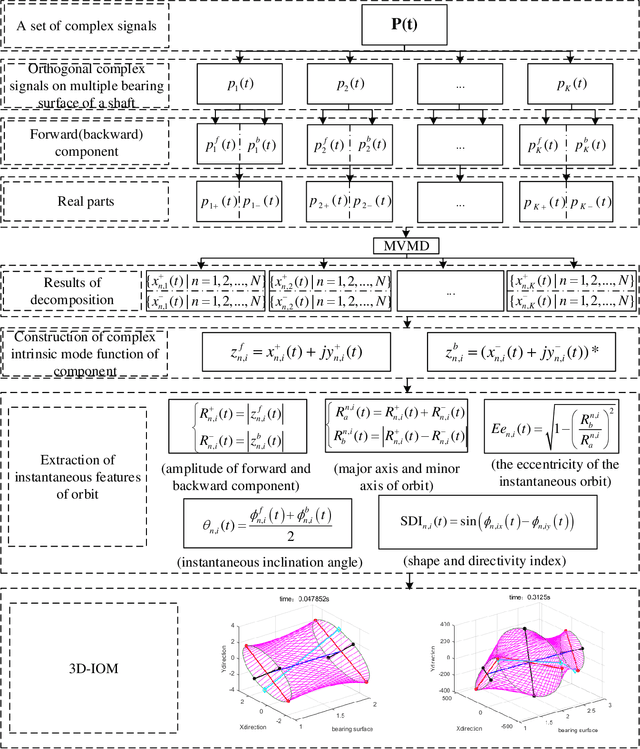
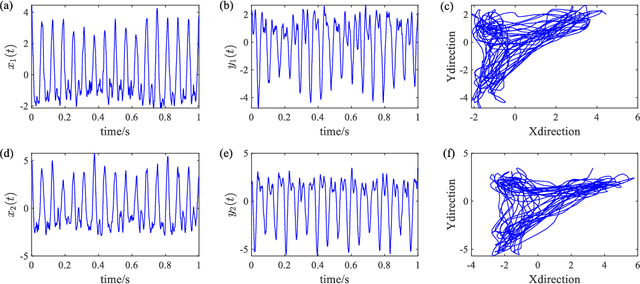
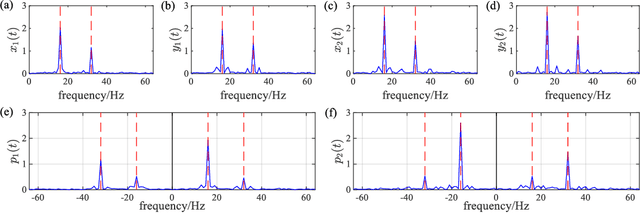
Full spectrum and holospectrum are homogenous information fusion technology developed for the fault diagnosis of rotating machinery and are often used in the analysis of the orbit of rotating machinery. However, both of the techniques are based on Fourier transform, so they can only handle stationary signals, which limits their development. By drawing inspiration from the approach of multivariate variational mode decomposition (MVMD) and the complex-valued signal decomposition, we propose a method called multivariate complex variational mode decomposition (MCVMD) for processing non-stationary complex-valued signals of multi-dimensional bearing surfaces in this work. In particular, the proposed method takes the advantages of the joint information between the complex-valued signals of multi-dimensional bearing surfaces, and owing to this property, we provide its three-dimensional instantaneous orbit map (3D-IOM) to present the overall perspective of the rotor-bearing system and also offer a high-resolution time-full spectrum (Time-FS) to display the forward and backward frequency components of all the bearing surfaces within a time-frequency plane. The effectiveness of the proposed method through both the simulated experiment and the real-life complex-valued signals are shown in this paper.

A Homotopic Method to Solve the Lasso Problems with an Improved Upper Bound of Convergence Rate

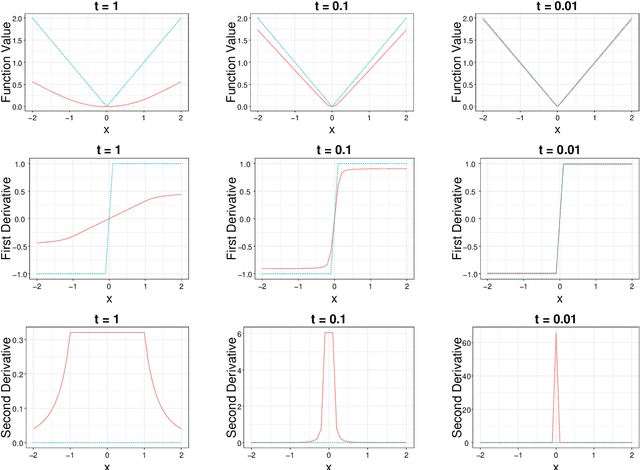
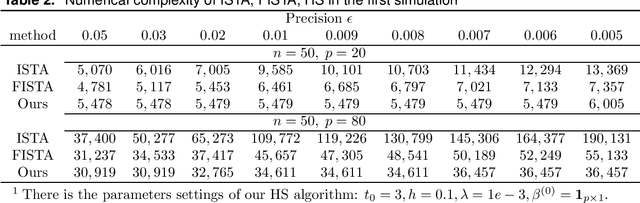
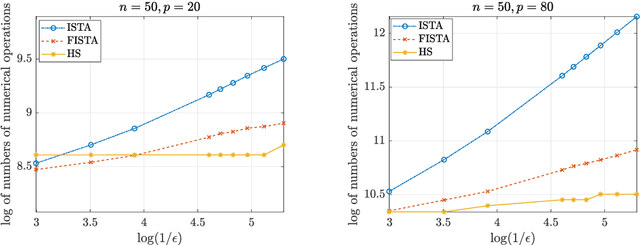
In optimization, it is known that when the objective functions are strictly convex and well-conditioned, gradient based approaches can be extremely effective, e.g., achieving the exponential rate in convergence. On the other hand, the existing Lasso-type of estimator in general cannot achieve the optimal rate due to the undesirable behavior of the absolute function at the origin. A homotopic method is to use a sequence of surrogate functions to approximate the $\ell_1$ penalty that is used in the Lasso-type of estimators. The surrogate functions will converge to the $\ell_1$ penalty in the Lasso estimator. At the same time, each surrogate function is strictly convex, which enables provable faster numerical rate of convergence. In this paper, we demonstrate that by meticulously defining the surrogate functions, one can prove faster numerical convergence rate than any existing methods in computing for the Lasso-type of estimators. Namely, the state-of-the-art algorithms can only guarantee $O(1/\epsilon)$ or $O(1/\sqrt{\epsilon})$ convergence rates, while we can prove an $O([\log(1/\epsilon)]^2)$ for the newly proposed algorithm. Our numerical simulations show that the new algorithm also performs better empirically.