Training Physical Neural Networks for Analog In-Memory Computing

In-memory computing (IMC) architectures mitigate the von Neumann bottleneck encountered in traditional deep learning accelerators. Its energy efficiency can realize deep learning-based edge applications. However, because IMC is implemented using analog circuits, inherent non-idealities in the hardware pose significant challenges. This paper presents physical neural networks (PNNs) for constructing physical models of IMC. PNNs can address the synaptic current's dependence on membrane potential, a challenge in charge-domain IMC systems. The proposed model is mathematically equivalent to spiking neural networks with reversal potentials. With a novel technique called differentiable spike-time discretization, the PNNs are efficiently trained. We show that hardware non-idealities traditionally viewed as detrimental can enhance the model's learning performance. This bottom-up methodology was validated by designing an IMC circuit with non-ideal characteristics using the sky130 process. When employing this bottom-up approach, the modeling error reduced by an order of magnitude compared to conventional top-down methods in post-layout simulations.

Learning Deep Dissipative Dynamics

This study challenges strictly guaranteeing ``dissipativity'' of a dynamical system represented by neural networks learned from given time-series data. Dissipativity is a crucial indicator for dynamical systems that generalizes stability and input-output stability, known to be valid across various systems including robotics, biological systems, and molecular dynamics. By analytically proving the general solution to the nonlinear Kalman-Yakubovich-Popov (KYP) lemma, which is the necessary and sufficient condition for dissipativity, we propose a differentiable projection that transforms any dynamics represented by neural networks into dissipative ones and a learning method for the transformed dynamics. Utilizing the generality of dissipativity, our method strictly guarantee stability, input-output stability, and energy conservation of trained dynamical systems. Finally, we demonstrate the robustness of our method against out-of-domain input through applications to robotic arms and fluid dynamics. Code here https://github.com/kojima-r/DeepDissipativeModel

A New Deep State-Space Analysis Framework for Patient Latent State Estimation and Classification from EHR Time Series Data

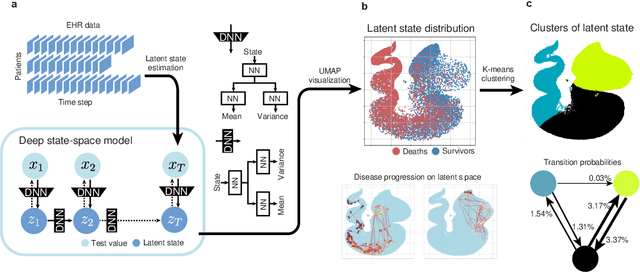
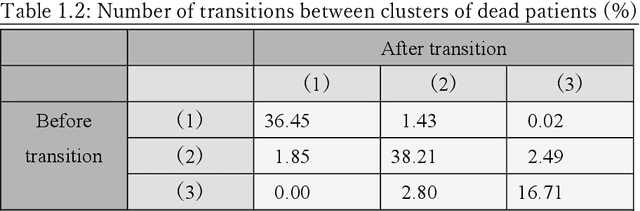
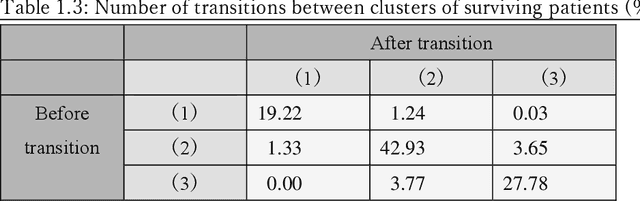
Many diseases, including cancer and chronic conditions, require extended treatment periods and long-term strategies. Machine learning and AI research focusing on electronic health records (EHRs) have emerged to address this need. Effective treatment strategies involve more than capturing sequential changes in patient test values. It requires an explainable and clinically interpretable model by capturing the patient's internal state over time. In this study, we propose the "deep state-space analysis framework," using time-series unsupervised learning of EHRs with a deep state-space model. This framework enables learning, visualizing, and clustering of temporal changes in patient latent states related to disease progression. We evaluated our framework using time-series laboratory data from 12,695 cancer patients. By estimating latent states, we successfully discover latent states related to prognosis. By visualization and cluster analysis, the temporal transition of patient status and test items during state transitions characteristic of each anticancer drug were identified. Our framework surpasses existing methods in capturing interpretable latent space. It can be expected to enhance our comprehension of disease progression from EHRs, aiding treatment adjustments and prognostic determinations.

Learning Deep Input-Output Stable Dynamics

Learning stable dynamics from observed time-series data is an essential problem in robotics, physical modeling, and systems biology. Many of these dynamics are represented as an inputs-output system to communicate with the external environment. In this study, we focus on input-output stable systems, exhibiting robustness against unexpected stimuli and noise. We propose a method to learn nonlinear systems guaranteeing the input-output stability. Our proposed method utilizes the differentiable projection onto the space satisfying the Hamilton-Jacobi inequality to realize the input-output stability. The problem of finding this projection can be formulated as a quadratic constraint quadratic programming problem, and we derive the particular solution analytically. Also, we apply our method to a toy bistable model and the task of training a benchmark generated from a glucose-insulin simulator. The results show that the nonlinear system with neural networks by our method achieves the input-output stability, unlike naive neural networks. Our code is available at https://github.com/clinfo/DeepIOStability.