Training Physical Neural Networks for Analog In-Memory Computing

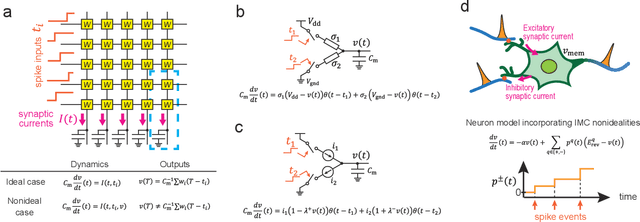
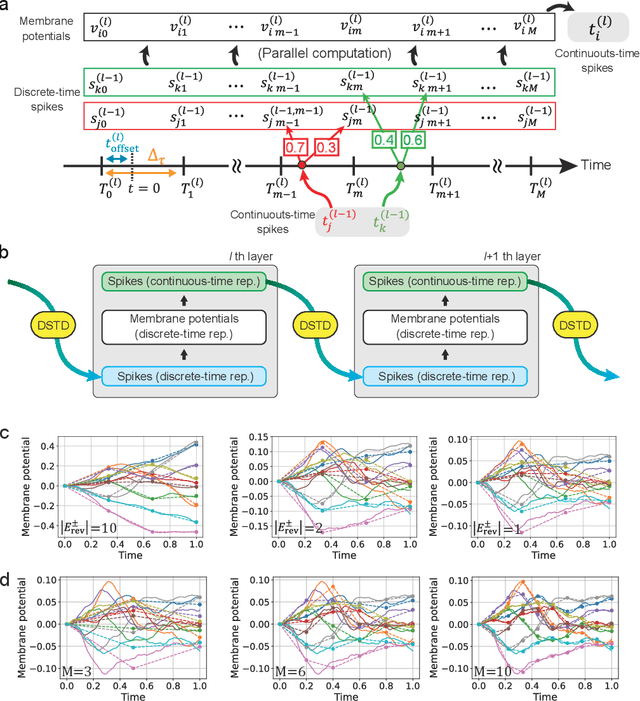
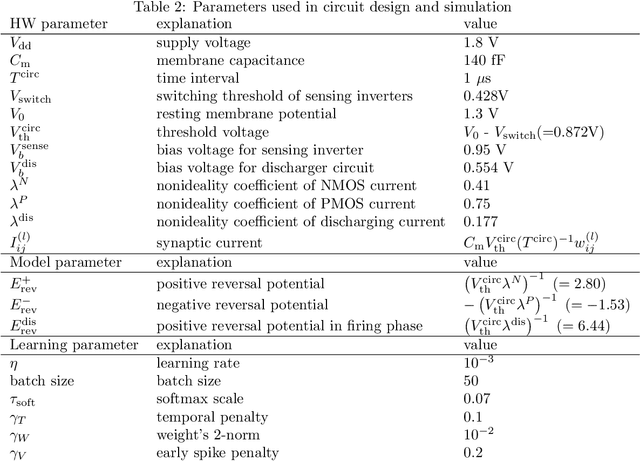
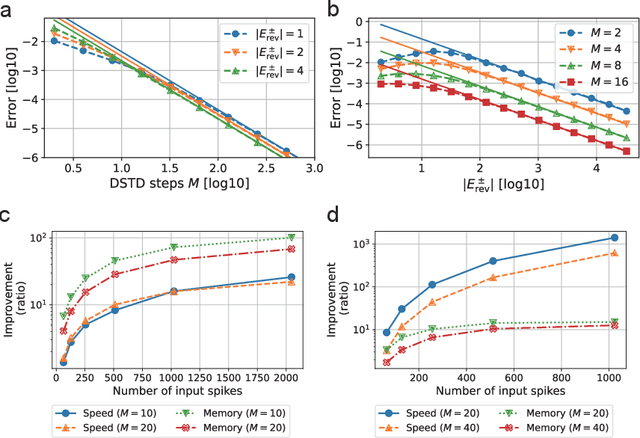
In-memory computing (IMC) architectures mitigate the von Neumann bottleneck encountered in traditional deep learning accelerators. Its energy efficiency can realize deep learning-based edge applications. However, because IMC is implemented using analog circuits, inherent non-idealities in the hardware pose significant challenges. This paper presents physical neural networks (PNNs) for constructing physical models of IMC. PNNs can address the synaptic current's dependence on membrane potential, a challenge in charge-domain IMC systems. The proposed model is mathematically equivalent to spiking neural networks with reversal potentials. With a novel technique called differentiable spike-time discretization, the PNNs are efficiently trained. We show that hardware non-idealities traditionally viewed as detrimental can enhance the model's learning performance. This bottom-up methodology was validated by designing an IMC circuit with non-ideal characteristics using the sky130 process. When employing this bottom-up approach, the modeling error reduced by an order of magnitude compared to conventional top-down methods in post-layout simulations.

Sparse-firing regularization methods for spiking neural networks with time-to-first spike coding

The training of multilayer spiking neural networks (SNNs) using the error backpropagation algorithm has made significant progress in recent years. Among the various training schemes, the error backpropagation method that directly uses the firing time of neurons has attracted considerable attention because it can realize ideal temporal coding. This method uses time-to-first spike (TTFS) coding, in which each neuron fires at most once, and this restriction on the number of firings enables information to be processed at a very low firing frequency. This low firing frequency increases the energy efficiency of information processing in SNNs, which is important not only because of its similarity with information processing in the brain, but also from an engineering point of view. However, only an upper limit has been provided for TTFS-coded SNNs, and the information-processing capability of SNNs at lower firing frequencies has not been fully investigated. In this paper, we propose two spike timing-based sparse-firing (SSR) regularization methods to further reduce the firing frequency of TTFS-coded SNNs. The first is the membrane potential-aware SSR (M-SSR) method, which has been derived as an extreme form of the loss function of the membrane potential value. The second is the firing condition-aware SSR (F-SSR) method, which is a regularization function obtained from the firing conditions. Both methods are characterized by the fact that they only require information about the firing timing and associated weights. The effects of these regularization methods were investigated on the MNIST, Fashion-MNIST, and CIFAR-10 datasets using multilayer perceptron networks and convolutional neural network structures.

Effects of VLSI Circuit Constraints on Temporal-Coding Multilayer Spiking Neural Networks

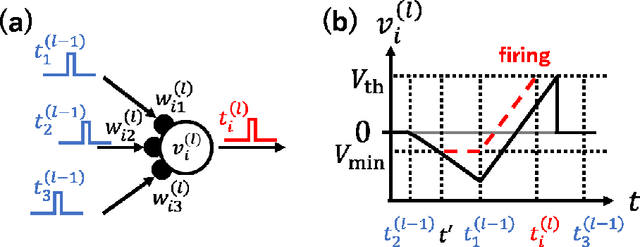
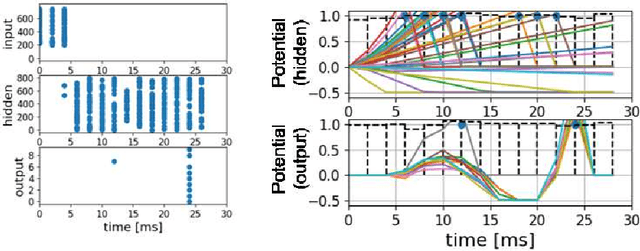
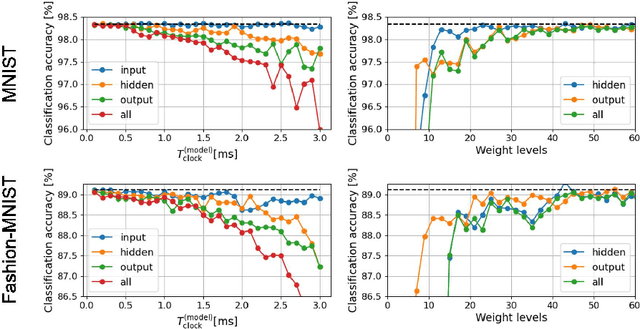
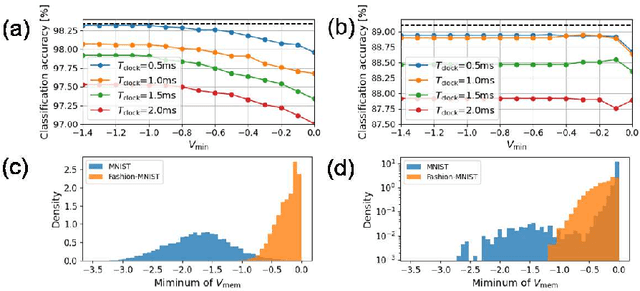
The spiking neural network (SNN) has been attracting considerable attention not only as a mathematical model for the brain, but also as an energy-efficient information processing model for real-world applications. In particular, SNNs based on temporal coding are expected to be much more efficient than those based on rate coding, because the former requires substantially fewer spikes to carry out tasks. As SNNs are continuous-state and continuous-time models, it is favorable to implement them with analog VLSI circuits. However, the construction of the entire system with continuous-time analog circuits would be infeasible when the system size is very large. Therefore, mixed-signal circuits must be employed, and the time discretization and quantization of the synaptic weights are necessary. Moreover, the analog VLSI implementation of SNNs exhibits non-idealities, such as the effects of noise and device mismatches, as well as other constraints arising from the analog circuit operation. In this study, we investigated the effects of the time discretization and/or weight quantization on the performance of SNNs. Furthermore, we elucidated the effects the lower bound of the membrane potentials and the temporal fluctuation of the firing threshold. Finally, we propose an optimal approach for the mapping of mathematical SNN models to analog circuits with discretized time.