Unsupervised Spatial-spectral Network Learning for Hyperspectral Compressive Snapshot Reconstruction

Hyperspectral compressive imaging takes advantage of compressive sensing theory to achieve coded aperture snapshot measurement without temporal scanning, and the entire three-dimensional spatial-spectral data is captured by a two-dimensional projection during a single integration period. Its core issue is how to reconstruct the underlying hyperspectral image using compressive sensing reconstruction algorithms. Due to the diversity in the spectral response characteristics and wavelength range of different spectral imaging devices, previous works are often inadequate to capture complex spectral variations or lack the adaptive capacity to new hyperspectral imagers. In order to address these issues, we propose an unsupervised spatial-spectral network to reconstruct hyperspectral images only from the compressive snapshot measurement. The proposed network acts as a conditional generative model conditioned on the snapshot measurement, and it exploits the spatial-spectral attention module to capture the joint spatial-spectral correlation of hyperspectral images. The network parameters are optimized to make sure that the network output can closely match the given snapshot measurement according to the imaging model, thus the proposed network can adapt to different imaging settings, which can inherently enhance the applicability of the network. Extensive experiments upon multiple datasets demonstrate that our network can achieve better reconstruction results than the state-of-the-art methods.

Fast and Robust Subspace Clustering Using Random Projections

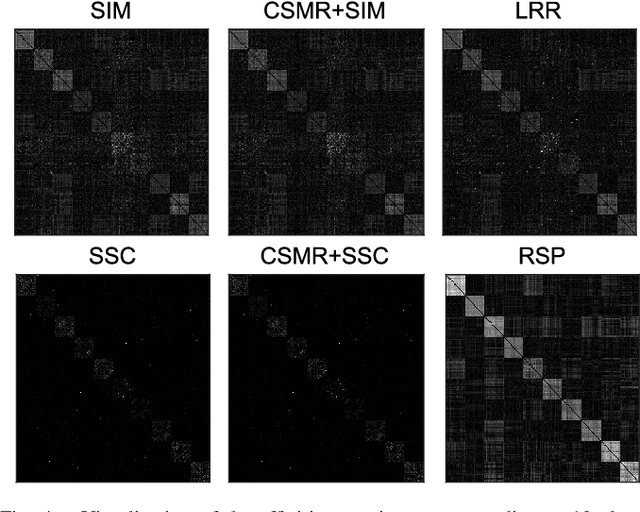
Over the past several decades, subspace clustering has been receiving increasing interest and continuous progress. However, due to the lack of scalability and/or robustness, existing methods still have difficulty in dealing with the data that possesses simultaneously three characteristics: high-dimensional, massive and grossly corrupted. To tackle the scalability and robustness issues simultaneously, in this paper we suggest to consider a problem called compressive robust subspace clustering, which is to perform robust subspace clustering with the compressed data, and which is generated by projecting the original high-dimensional data onto a lower-dimensional subspace chosen at random. Given these random projections, the proposed method, row space pursuit (RSP), recovers not only the authentic row space, which provably leads to correct clustering results under certain conditions, but also the gross errors possibly existing in data. The compressive nature of the random projections gives our RSP high computational and storage efficiency, and the recovery property enables the ability for RSP to deal with the grossly corrupted data. Extensive experiments on high-dimensional and/or large-scale datasets show that RSP can maintain comparable accuracies to to prevalent methods with significant reductions in the computational time.

Graph Regularized Low Rank Representation for Aerosol Optical Depth Retrieval

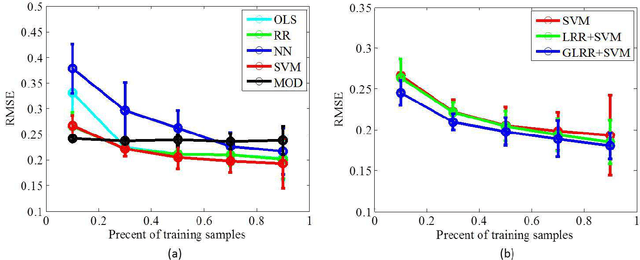
In this paper, we propose a novel data-driven regression model for aerosol optical depth (AOD) retrieval. First, we adopt a low rank representation (LRR) model to learn a powerful representation of the spectral response. Then, graph regularization is incorporated into the LRR model to capture the local structure information and the nonlinear property of the remote-sensing data. Since it is easy to acquire the rich satellite-retrieval results, we use them as a baseline to construct the graph. Finally, the learned feature representation is feeded into support vector machine (SVM) to retrieve AOD. Experiments are conducted on two widely used data sets acquired by different sensors, and the experimental results show that the proposed method can achieve superior performance compared to the physical models and other state-of-the-art empirical models.

Elastic Net Hypergraph Learning for Image Clustering and Semi-supervised Classification

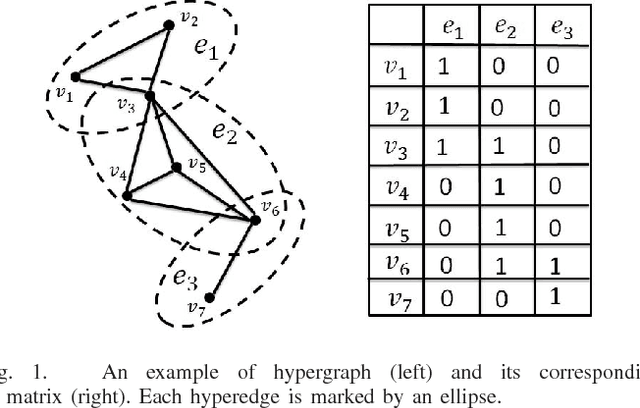
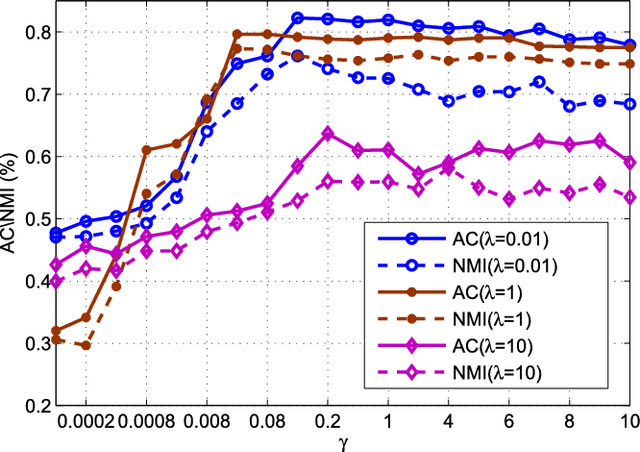
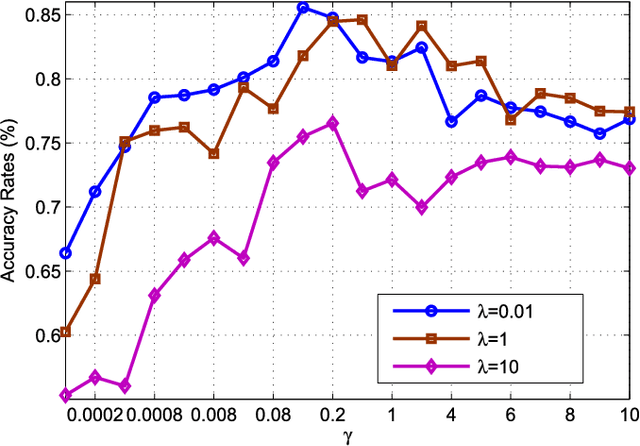
Graph model is emerging as a very effective tool for learning the complex structures and relationships hidden in data. Generally, the critical purpose of graph-oriented learning algorithms is to construct an informative graph for image clustering and classification tasks. In addition to the classical $K$-nearest-neighbor and $r$-neighborhood methods for graph construction, $l_1$-graph and its variants are emerging methods for finding the neighboring samples of a center datum, where the corresponding ingoing edge weights are simultaneously derived by the sparse reconstruction coefficients of the remaining samples. However, the pair-wise links of $l_1$-graph are not capable of capturing the high order relationships between the center datum and its prominent data in sparse reconstruction. Meanwhile, from the perspective of variable selection, the $l_1$ norm sparse constraint, regarded as a LASSO model, tends to select only one datum from a group of data that are highly correlated and ignore the others. To simultaneously cope with these drawbacks, we propose a new elastic net hypergraph learning model, which consists of two steps. In the first step, the Robust Matrix Elastic Net model is constructed to find the canonically related samples in a somewhat greedy way, achieving the grouping effect by adding the $l_2$ penalty to the $l_1$ constraint. In the second step, hypergraph is used to represent the high order relationships between each datum and its prominent samples by regarding them as a hyperedge. Subsequently, hypergraph Laplacian matrix is constructed for further analysis. New hypergraph learning algorithms, including unsupervised clustering and multi-class semi-supervised classification, are then derived. Extensive experiments on face and handwriting databases demonstrate the effectiveness of the proposed method.