Elastic Net Hypergraph Learning for Image Clustering and Semi-supervised Classification
Paper and Code
Mar 03, 2016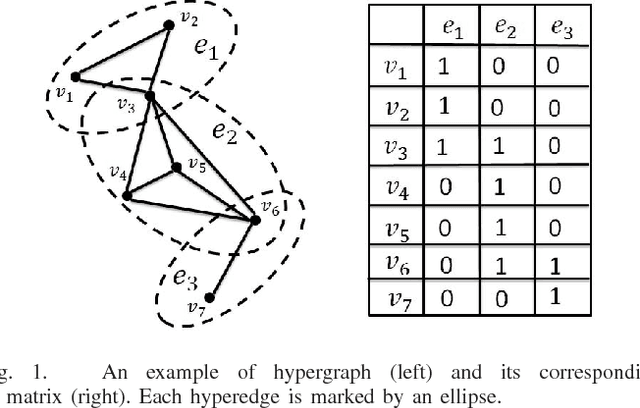

Graph model is emerging as a very effective tool for learning the complex structures and relationships hidden in data. Generally, the critical purpose of graph-oriented learning algorithms is to construct an informative graph for image clustering and classification tasks. In addition to the classical $K$-nearest-neighbor and $r$-neighborhood methods for graph construction, $l_1$-graph and its variants are emerging methods for finding the neighboring samples of a center datum, where the corresponding ingoing edge weights are simultaneously derived by the sparse reconstruction coefficients of the remaining samples. However, the pair-wise links of $l_1$-graph are not capable of capturing the high order relationships between the center datum and its prominent data in sparse reconstruction. Meanwhile, from the perspective of variable selection, the $l_1$ norm sparse constraint, regarded as a LASSO model, tends to select only one datum from a group of data that are highly correlated and ignore the others. To simultaneously cope with these drawbacks, we propose a new elastic net hypergraph learning model, which consists of two steps. In the first step, the Robust Matrix Elastic Net model is constructed to find the canonically related samples in a somewhat greedy way, achieving the grouping effect by adding the $l_2$ penalty to the $l_1$ constraint. In the second step, hypergraph is used to represent the high order relationships between each datum and its prominent samples by regarding them as a hyperedge. Subsequently, hypergraph Laplacian matrix is constructed for further analysis. New hypergraph learning algorithms, including unsupervised clustering and multi-class semi-supervised classification, are then derived. Extensive experiments on face and handwriting databases demonstrate the effectiveness of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge