Fast and Robust Subspace Clustering Using Random Projections

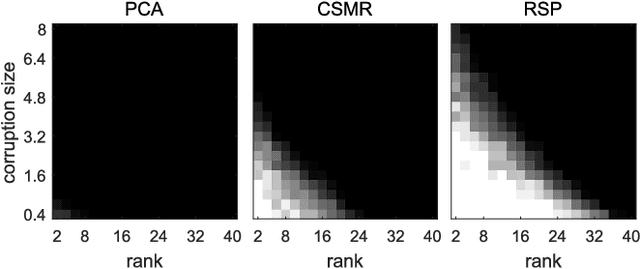
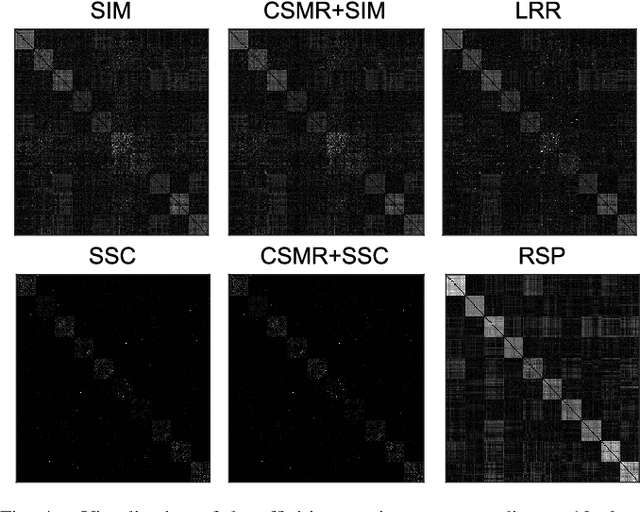
Over the past several decades, subspace clustering has been receiving increasing interest and continuous progress. However, due to the lack of scalability and/or robustness, existing methods still have difficulty in dealing with the data that possesses simultaneously three characteristics: high-dimensional, massive and grossly corrupted. To tackle the scalability and robustness issues simultaneously, in this paper we suggest to consider a problem called compressive robust subspace clustering, which is to perform robust subspace clustering with the compressed data, and which is generated by projecting the original high-dimensional data onto a lower-dimensional subspace chosen at random. Given these random projections, the proposed method, row space pursuit (RSP), recovers not only the authentic row space, which provably leads to correct clustering results under certain conditions, but also the gross errors possibly existing in data. The compressive nature of the random projections gives our RSP high computational and storage efficiency, and the recovery property enables the ability for RSP to deal with the grossly corrupted data. Extensive experiments on high-dimensional and/or large-scale datasets show that RSP can maintain comparable accuracies to to prevalent methods with significant reductions in the computational time.