Toward AI-Driven Digital Twins for Metropolitan Floods: A Conditional Latent Dynamics Network Surrogate of the Shallow Water Equations

AI-driven flood digital twins demand fast hydrodynamic surrogates for ensemble forecasting and observation assimilation. Yet even GPU-accelerated two-dimensional shallow water equation (SWE) solvers still require $\sim 55$ minutes per $96$-hour run on a $\sim 4.2$-million-active-cell metropolitan basin (the Des~Plaines River basin at $30\,\mathrm{m}$ resolution), making such workloads prohibitive at native resolution. We present the Conditional Latent Dynamics Network (CLDNet): a low-dimensional latent neural ODE driven by rainfall, paired with a coordinate-based decoder conditioned on static terrain (elevation, slope, Manning roughness) that reconstructs depth and discharge at arbitrary query points. Pointwise decoding decouples memory from grid size and handles irregular watersheds natively, enabling metropolitan-scale training on a single compute node and direct queries at exact gauge coordinates without raster snapping. We evaluate CLDNet on a synthetic $250{,}000$-cell Texas benchmark and on a new Des~Plaines case study of $114$ real-rainfall Stage~IV storms whose reference simulator we validate against United States Geological Survey (USGS) gauges at the April~2013 flood-of-record (Nash--Sutcliffe efficiency $0.57$--$0.94$ on mean-recentered water-surface elevation). CLDNet roughly halves the relative root-mean-squared error of an unconditional baseline, outperforms regular-grid VAE--ConvLSTM and FNO baselines on the Texas benchmark (both presuppose a Cartesian grid and do not apply to the irregular Des~Plaines watershed), reaches a critical success index of $\approx 86\%$ at the $0.5\,\mathrm{m}$ inundation threshold, and produces a full $96$-hour basin-wide forecast in $\sim 29$ seconds -- a $\sim 115\times$ speedup.

Variationally correct operator learning: Reduced basis neural operator with a posteriori error estimation

Minimizing PDE-residual losses is a common strategy to promote physical consistency in neural operators. However, standard formulations often lack variational correctness, meaning that small residuals do not guarantee small solution errors due to the use of non-compliant norms or ad hoc penalty terms for boundary conditions. This work develops a variationally correct operator learning framework by constructing first-order system least-squares (FOSLS) objectives whose values are provably equivalent to the solution error in PDE-induced norms. We demonstrate this framework on stationary diffusion and linear elasticity, incorporating mixed Dirichlet-Neumann boundary conditions via variational lifts to preserve norm equivalence without inconsistent penalties. To ensure the function space conformity required by the FOSLS loss, we propose a Reduced Basis Neural Operator (RBNO). The RBNO predicts coefficients for a pre-computed, conforming reduced basis, thereby ensuring variational stability by design while enabling efficient training. We provide a rigorous convergence analysis that bounds the total error by the sum of finite element discretization bias, reduced basis truncation error, neural network approximation error, and statistical estimation errors arising from finite sampling and optimization. Numerical benchmarks validate these theoretical bounds and demonstrate that the proposed approach achieves superior accuracy in PDE-compliant norms compared to standard baselines, while the residual loss serves as a reliable, computable a posteriori error estimator.

Adaptive Inner Speech-Text Alignment for LLM-based Speech Translation

Recent advancement of large language models (LLMs) has led to significant breakthroughs across various tasks, laying the foundation for the development of LLM-based speech translation systems. Existing methods primarily focus on aligning inputs and outputs across modalities while overlooking deeper semantic alignment within model representations. To address this limitation, we propose an Adaptive Inner Speech-Text Alignment (AI-STA) method to bridge the modality gap by explicitly aligning speech and text representations at selected layers within LLMs. To achieve this, we leverage the optimal transport (OT) theory to quantify fine-grained representation discrepancies between speech and text. Furthermore, we utilize the cross-modal retrieval technique to identify the layers that are best suited for alignment and perform joint training on these layers. Experimental results on speech translation (ST) tasks demonstrate that AI-STA significantly improves the translation performance of large speech-text models (LSMs), outperforming previous state-of-the-art approaches. Our findings highlight the importance of inner-layer speech-text alignment in LLMs and provide new insights into enhancing cross-modal learning.

Derivative-enhanced Deep Operator Network

Deep operator networks (DeepONets), a class of neural operators that learn mappings between function spaces, have recently been developed as surrogate models for parametric partial differential equations (PDEs). In this work we propose a derivative-enhanced deep operator network (DE-DeepONet), which leverages the derivative information to enhance the prediction accuracy, and provide a more accurate approximation of the derivatives, especially when the training data are limited. DE-DeepONet incorporates dimension reduction of input into DeepONet and includes two types of derivative labels in the loss function for training, that is, the directional derivatives of the output function with respect to the input function and the gradient of the output function with respect to the physical domain variables. We test DE-DeepONet on three different equations with increasing complexity to demonstrate its effectiveness compared to the vanilla DeepONet.

Truthful Generalized Linear Models

In this paper we study estimating Generalized Linear Models (GLMs) in the case where the agents (individuals) are strategic or self-interested and they concern about their privacy when reporting data. Compared with the classical setting, here we aim to design mechanisms that can both incentivize most agents to truthfully report their data and preserve the privacy of individuals' reports, while their outputs should also close to the underlying parameter. In the first part of the paper, we consider the case where the covariates are sub-Gaussian and the responses are heavy-tailed where they only have the finite fourth moments. First, motivated by the stationary condition of the maximizer of the likelihood function, we derive a novel private and closed form estimator. Based on the estimator, we propose a mechanism which has the following properties via some appropriate design of the computation and payment scheme for several canonical models such as linear regression, logistic regression and Poisson regression: (1) the mechanism is $o(1)$-jointly differentially private (with probability at least $1-o(1)$); (2) it is an $o(\frac{1}{n})$-approximate Bayes Nash equilibrium for a $(1-o(1))$-fraction of agents to truthfully report their data, where $n$ is the number of agents; (3) the output could achieve an error of $o(1)$ to the underlying parameter; (4) it is individually rational for a $(1-o(1))$ fraction of agents in the mechanism ; (5) the payment budget required from the analyst to run the mechanism is $o(1)$. In the second part, we consider the linear regression model under more general setting where both covariates and responses are heavy-tailed and only have finite fourth moments. By using an $\ell_4$-norm shrinkage operator, we propose a private estimator and payment scheme which have similar properties as in the sub-Gaussian case.

Frequency Estimation Under Multiparty Differential Privacy: One-shot and Streaming

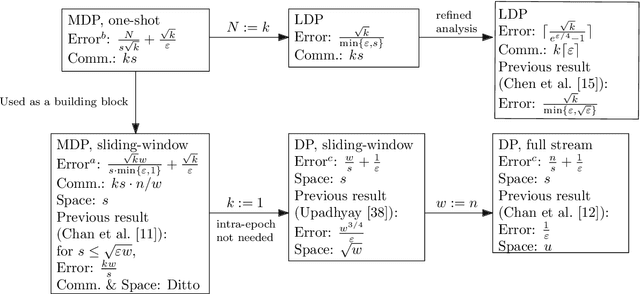
We study the fundamental problem of frequency estimation under both privacy and communication constraints, where the data is distributed among $k$ parties. We consider two application scenarios: (1) one-shot, where the data is static and the aggregator conducts a one-time computation; and (2) streaming, where each party receives a stream of items over time and the aggregator continuously monitors the frequencies. We adopt the model of multiparty differential privacy (MDP), which is more general than local differential privacy (LDP) and (centralized) differential privacy. Our protocols achieve optimality (up to logarithmic factors) permissible by the more stringent of the two constraints. In particular, when specialized to the $\varepsilon$-LDP model, our protocol achieves an error of $\sqrt{k}/(e^{\Theta(\varepsilon)}-1)$ for all $\varepsilon$, while the previous protocol (Chen et al., 2020) has error $O(\sqrt{k}/\min\{\varepsilon, \sqrt{\varepsilon}\})$.