Frequency Estimation Under Multiparty Differential Privacy: One-shot and Streaming
Paper and Code
Apr 05, 2021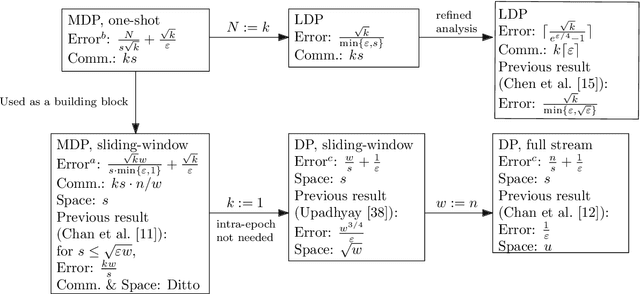



We study the fundamental problem of frequency estimation under both privacy and communication constraints, where the data is distributed among $k$ parties. We consider two application scenarios: (1) one-shot, where the data is static and the aggregator conducts a one-time computation; and (2) streaming, where each party receives a stream of items over time and the aggregator continuously monitors the frequencies. We adopt the model of multiparty differential privacy (MDP), which is more general than local differential privacy (LDP) and (centralized) differential privacy. Our protocols achieve optimality (up to logarithmic factors) permissible by the more stringent of the two constraints. In particular, when specialized to the $\varepsilon$-LDP model, our protocol achieves an error of $\sqrt{k}/(e^{\Theta(\varepsilon)}-1)$ for all $\varepsilon$, while the previous protocol (Chen et al., 2020) has error $O(\sqrt{k}/\min\{\varepsilon, \sqrt{\varepsilon}\})$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge