Yu-Hui Chen
Speed Is All You Need: On-Device Acceleration of Large Diffusion Models via GPU-Aware Optimizations
Apr 21, 2023Abstract:The rapid development and application of foundation models have revolutionized the field of artificial intelligence. Large diffusion models have gained significant attention for their ability to generate photorealistic images and support various tasks. On-device deployment of these models provides benefits such as lower server costs, offline functionality, and improved user privacy. However, common large diffusion models have over 1 billion parameters and pose challenges due to restricted computational and memory resources on devices. We present a series of implementation optimizations for large diffusion models that achieve the fastest reported inference latency to-date (under 12 seconds for Stable Diffusion 1.4 without int8 quantization on Samsung S23 Ultra for a 512x512 image with 20 iterations) on GPU-equipped mobile devices. These enhancements broaden the applicability of generative AI and improve the overall user experience across a wide range of devices.
Coercive Region-level Registration for Multi-modal Images
Nov 18, 2015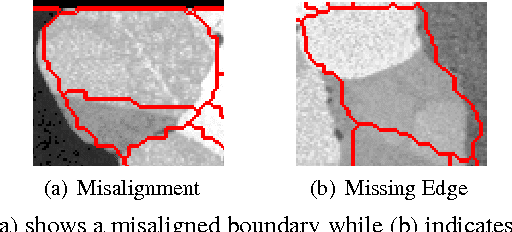
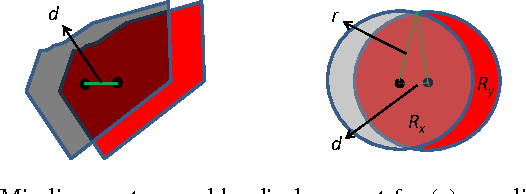
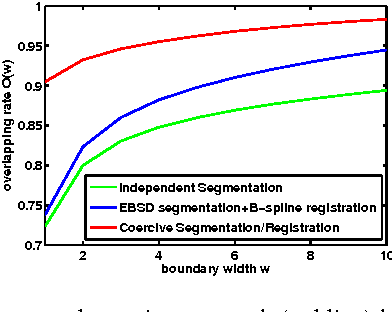

Abstract:We propose a coercive approach to simultaneously register and segment multi-modal images which share similar spatial structure. Registration is done at the region level to facilitate data fusion while avoiding the need for interpolation. The algorithm performs alternating minimization of an objective function informed by statistical models for pixel values in different modalities. Hypothesis tests are developed to determine whether to refine segmentations by splitting regions. We demonstrate that our approach has significantly better performance than the state-of-the-art registration and segmentation methods on microscopy images.
Multimodal MRI Neuroimaging with Motion Compensation Based on Particle Filtering
Nov 11, 2015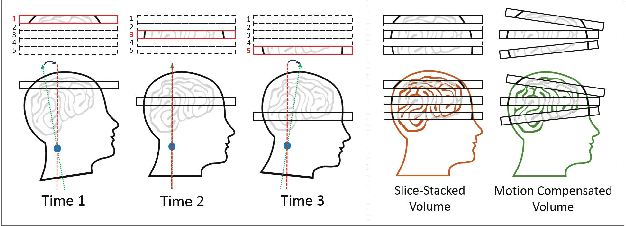
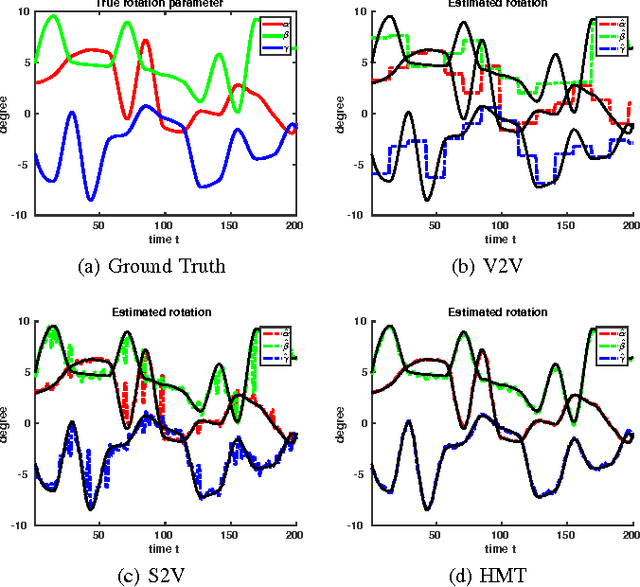
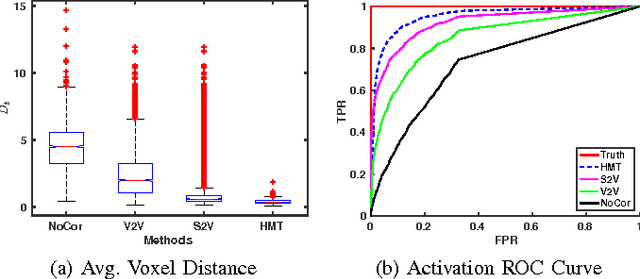
Abstract:Head movement during scanning impedes activation detection in fMRI studies. Head motion in fMRI acquired using slice-based Echo Planar Imaging (EPI) can be estimated and compensated by aligning the images onto a reference volume through image registration. However, registering EPI images volume to volume fails to consider head motion between slices, which may lead to severely biased head motion estimates. Slice-to-volume registration can be used to estimate motion parameters for each slice by more accurately representing the image acquisition sequence. However, accurate slice to volume mapping is dependent on the information content of the slices: middle slices are information rich, while edge slides are information poor and more prone to distortion. In this work, we propose a Gaussian particle filter based head motion tracking algorithm to reduce the image misregistration errors. The algorithm uses a dynamic state space model of head motion with an observation equation that models continuous slice acquisition of the scanner. Under this model the particle filter provides more accurate motion estimates and voxel position estimates. We demonstrate significant performance improvement of the proposed approach as compared to registration-only methods of head motion estimation and brain activation detection.
Statistical Estimation and Clustering of Group-invariant Orientation Parameters
May 22, 2015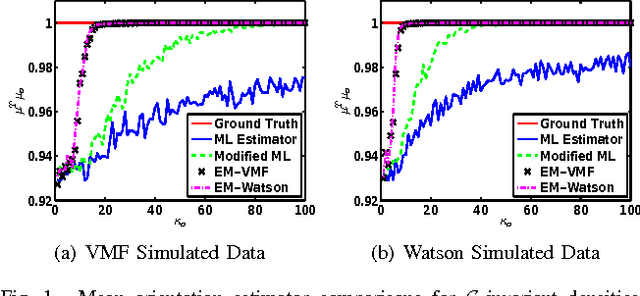

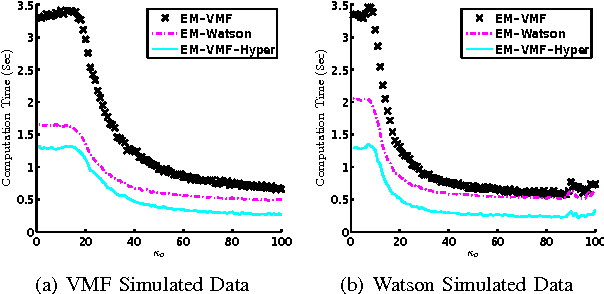

Abstract:We treat the problem of estimation of orientation parameters whose values are invariant to transformations from a spherical symmetry group. Previous work has shown that any such group-invariant distribution must satisfy a restricted finite mixture representation, which allows the orientation parameter to be estimated using an Expectation Maximization (EM) maximum likelihood (ML) estimation algorithm. In this paper, we introduce two parametric models for this spherical symmetry group estimation problem: 1) the hyperbolic Von Mises Fisher (VMF) mixture distribution and 2) the Watson mixture distribution. We also introduce a new EM-ML algorithm for clustering samples that come from mixtures of group-invariant distributions with different parameters. We apply the models to the problem of mean crystal orientation estimation under the spherically symmetric group associated with the crystal form, e.g., cubic or octahedral or hexahedral. Simulations and experiments establish the advantages of the extended EM-VMF and EM-Watson estimators for data acquired by Electron Backscatter Diffraction (EBSD) microscopy of a polycrystalline Nickel alloy sample.
A Dictionary Approach to EBSD Indexing
Feb 27, 2015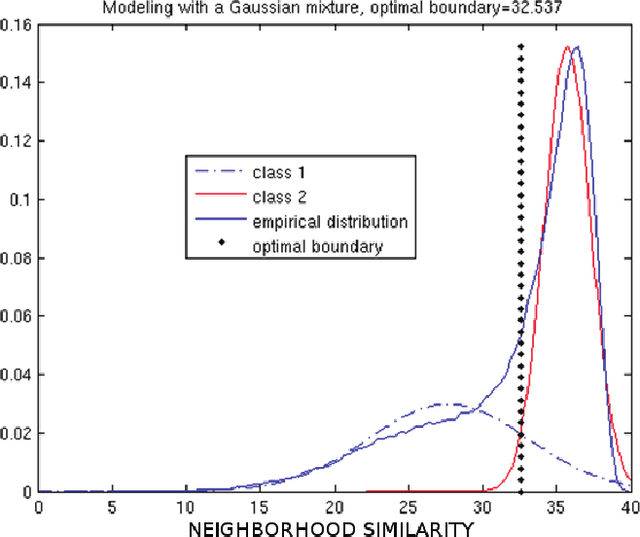
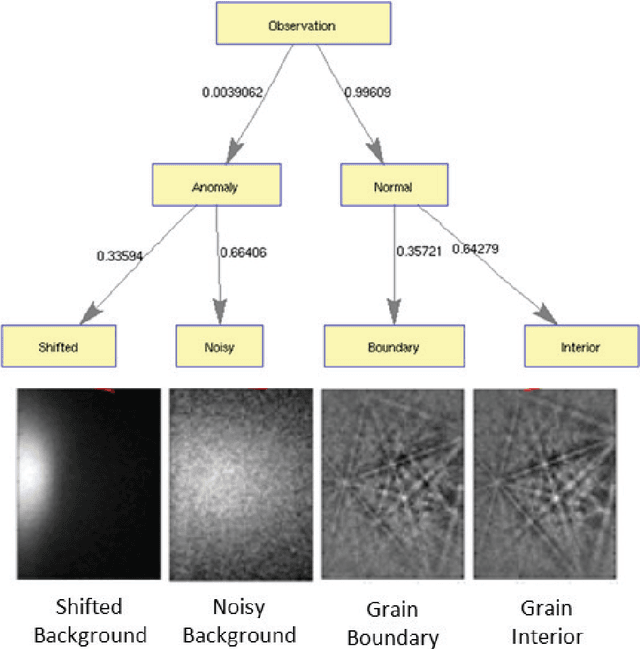

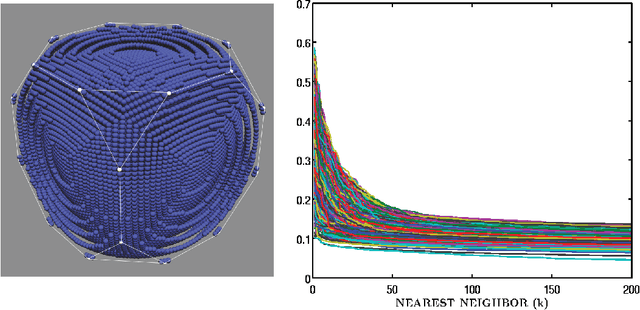
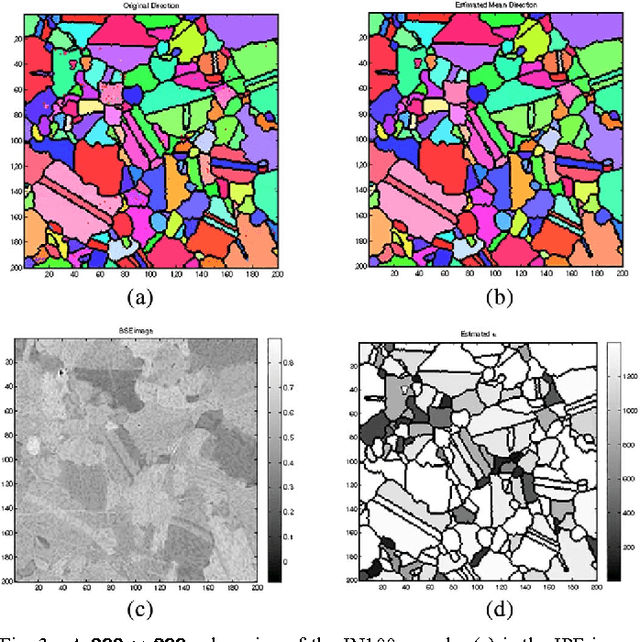
Abstract:We propose a framework for indexing of grain and sub-grain structures in electron backscatter diffraction (EBSD) images of polycrystalline materials. The framework is based on a previously introduced physics-based forward model by Callahan and De Graef (2013) relating measured patterns to grain orientations (Euler angle). The forward model is tuned to the microscope and the sample symmetry group. We discretize the domain of the forward model onto a dense grid of Euler angles and for each measured pattern we identify the most similar patterns in the dictionary. These patterns are used to identify boundaries, detect anomalies, and index crystal orientations. The statistical distribution of these closest matches is used in an unsupervised binary decision tree (DT) classifier to identify grain boundaries and anomalous regions. The DT classifies a pattern as an anomaly if it has an abnormally low similarity to any pattern in the dictionary. It classifies a pixel as being near a grain boundary if the highly ranked patterns in the dictionary differ significantly over the pixels 3x3 neighborhood. Indexing is accomplished by computing the mean orientation of the closest dictionary matches to each pattern. The mean orientation is estimated using a maximum likelihood approach that models the orientation distribution as a mixture of Von Mises-Fisher distributions over the quaternionic 3-sphere. The proposed dictionary matching approach permits segmentation, anomaly detection, and indexing to be performed in a unified manner with the additional benefit of uncertainty quantification. We demonstrate the proposed dictionary-based approach on a Ni-base IN100 alloy.
Parameter estimation in spherical symmetry groups
Dec 21, 2014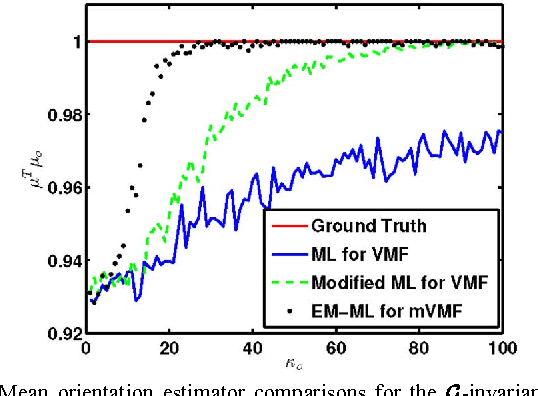
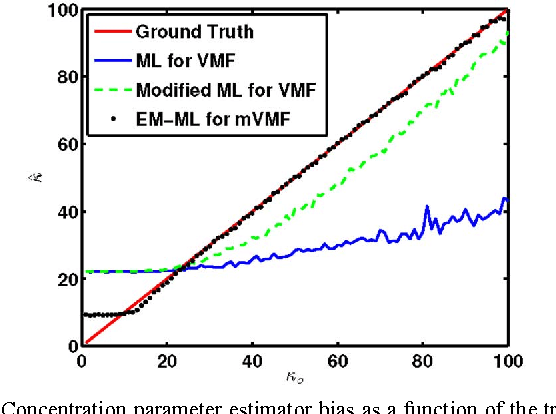
Abstract:This paper considers statistical estimation problems where the probability distribution of the observed random variable is invariant with respect to actions of a finite topological group. It is shown that any such distribution must satisfy a restricted finite mixture representation. When specialized to the case of distributions over the sphere that are invariant to the actions of a finite spherical symmetry group $\mathcal G$, a group-invariant extension of the Von Mises Fisher (VMF) distribution is obtained. The $\mathcal G$-invariant VMF is parameterized by location and scale parameters that specify the distribution's mean orientation and its concentration about the mean, respectively. Using the restricted finite mixture representation these parameters can be estimated using an Expectation Maximization (EM) maximum likelihood (ML) estimation algorithm. This is illustrated for the problem of mean crystal orientation estimation under the spherically symmetric group associated with the crystal form, e.g., cubic or octahedral or hexahedral. Simulations and experiments establish the advantages of the extended VMF EM-ML estimator for data acquired by Electron Backscatter Diffraction (EBSD) microscopy of a polycrystalline Nickel alloy sample.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge