Statistical Estimation and Clustering of Group-invariant Orientation Parameters

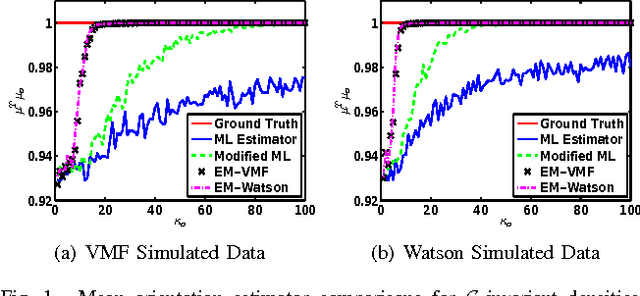
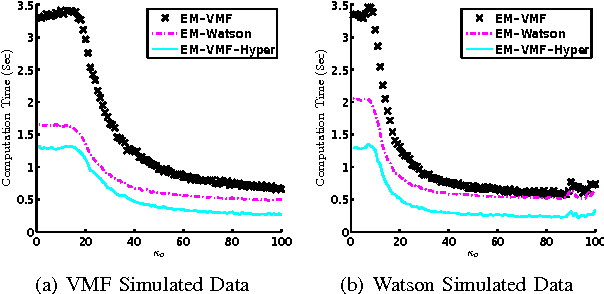
We treat the problem of estimation of orientation parameters whose values are invariant to transformations from a spherical symmetry group. Previous work has shown that any such group-invariant distribution must satisfy a restricted finite mixture representation, which allows the orientation parameter to be estimated using an Expectation Maximization (EM) maximum likelihood (ML) estimation algorithm. In this paper, we introduce two parametric models for this spherical symmetry group estimation problem: 1) the hyperbolic Von Mises Fisher (VMF) mixture distribution and 2) the Watson mixture distribution. We also introduce a new EM-ML algorithm for clustering samples that come from mixtures of group-invariant distributions with different parameters. We apply the models to the problem of mean crystal orientation estimation under the spherically symmetric group associated with the crystal form, e.g., cubic or octahedral or hexahedral. Simulations and experiments establish the advantages of the extended EM-VMF and EM-Watson estimators for data acquired by Electron Backscatter Diffraction (EBSD) microscopy of a polycrystalline Nickel alloy sample.

Parameter estimation in spherical symmetry groups

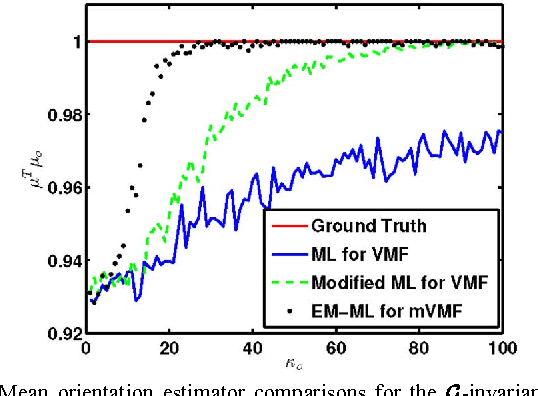
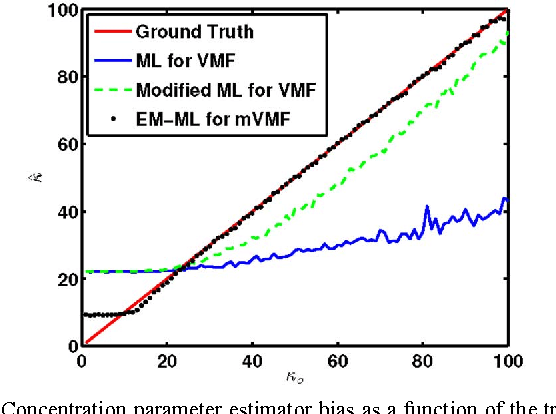
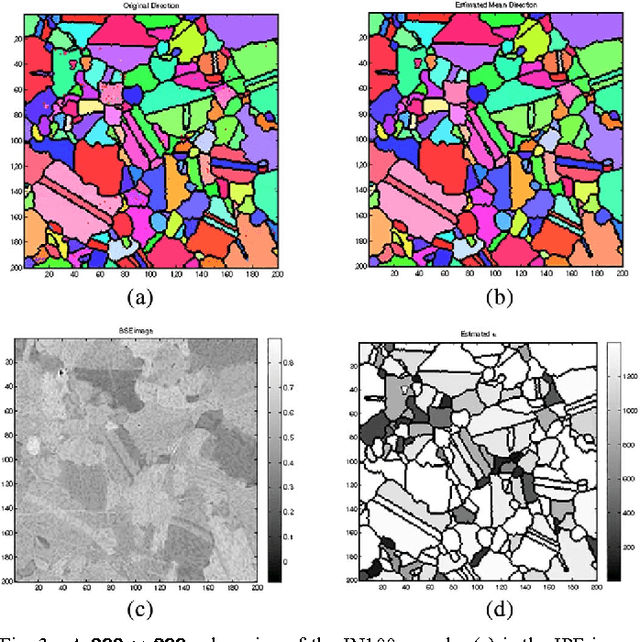
This paper considers statistical estimation problems where the probability distribution of the observed random variable is invariant with respect to actions of a finite topological group. It is shown that any such distribution must satisfy a restricted finite mixture representation. When specialized to the case of distributions over the sphere that are invariant to the actions of a finite spherical symmetry group $\mathcal G$, a group-invariant extension of the Von Mises Fisher (VMF) distribution is obtained. The $\mathcal G$-invariant VMF is parameterized by location and scale parameters that specify the distribution's mean orientation and its concentration about the mean, respectively. Using the restricted finite mixture representation these parameters can be estimated using an Expectation Maximization (EM) maximum likelihood (ML) estimation algorithm. This is illustrated for the problem of mean crystal orientation estimation under the spherically symmetric group associated with the crystal form, e.g., cubic or octahedral or hexahedral. Simulations and experiments establish the advantages of the extended VMF EM-ML estimator for data acquired by Electron Backscatter Diffraction (EBSD) microscopy of a polycrystalline Nickel alloy sample.