Coercive Region-level Registration for Multi-modal Images

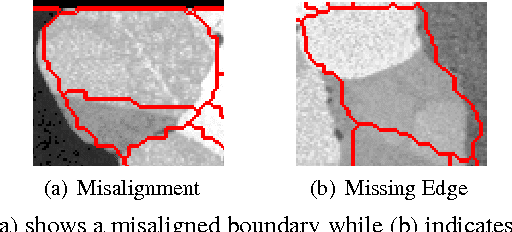
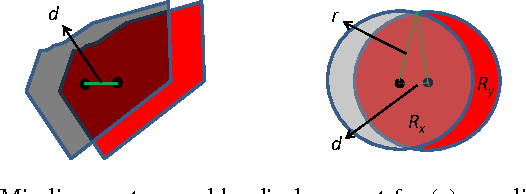
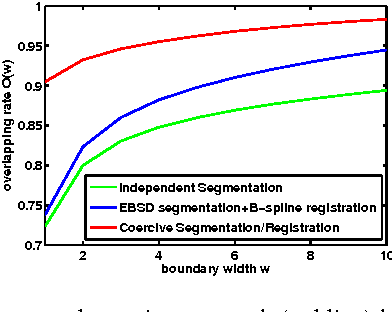
We propose a coercive approach to simultaneously register and segment multi-modal images which share similar spatial structure. Registration is done at the region level to facilitate data fusion while avoiding the need for interpolation. The algorithm performs alternating minimization of an objective function informed by statistical models for pixel values in different modalities. Hypothesis tests are developed to determine whether to refine segmentations by splitting regions. We demonstrate that our approach has significantly better performance than the state-of-the-art registration and segmentation methods on microscopy images.

Statistical Estimation and Clustering of Group-invariant Orientation Parameters

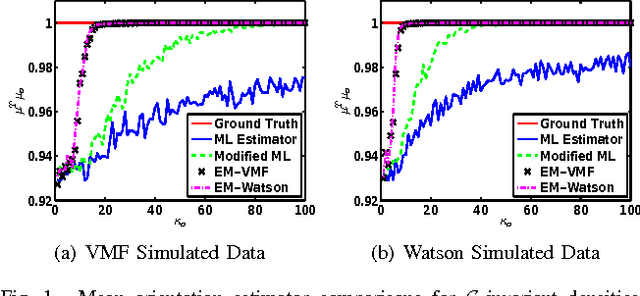
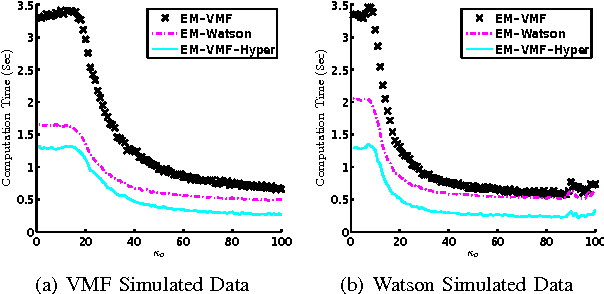
We treat the problem of estimation of orientation parameters whose values are invariant to transformations from a spherical symmetry group. Previous work has shown that any such group-invariant distribution must satisfy a restricted finite mixture representation, which allows the orientation parameter to be estimated using an Expectation Maximization (EM) maximum likelihood (ML) estimation algorithm. In this paper, we introduce two parametric models for this spherical symmetry group estimation problem: 1) the hyperbolic Von Mises Fisher (VMF) mixture distribution and 2) the Watson mixture distribution. We also introduce a new EM-ML algorithm for clustering samples that come from mixtures of group-invariant distributions with different parameters. We apply the models to the problem of mean crystal orientation estimation under the spherically symmetric group associated with the crystal form, e.g., cubic or octahedral or hexahedral. Simulations and experiments establish the advantages of the extended EM-VMF and EM-Watson estimators for data acquired by Electron Backscatter Diffraction (EBSD) microscopy of a polycrystalline Nickel alloy sample.

A Dictionary Approach to EBSD Indexing

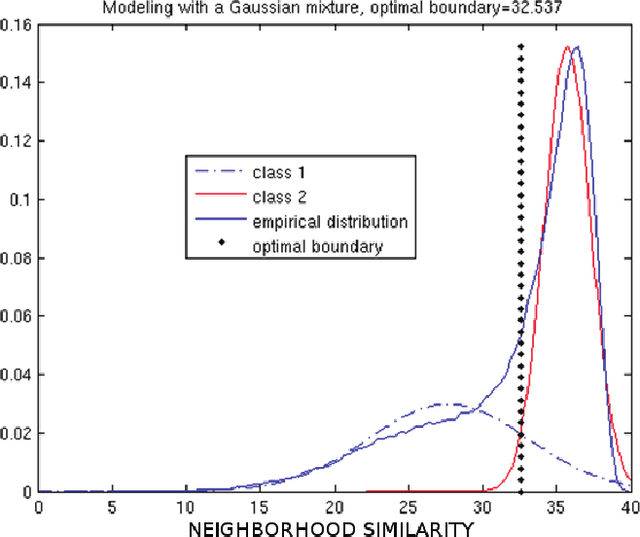
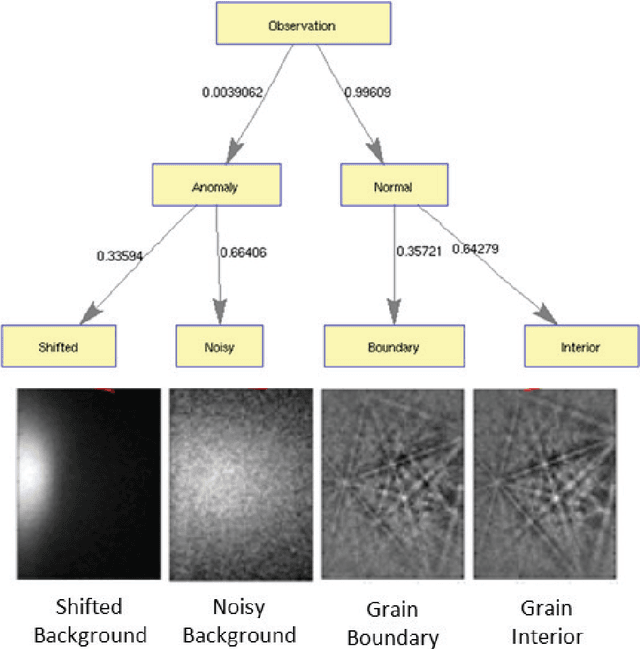
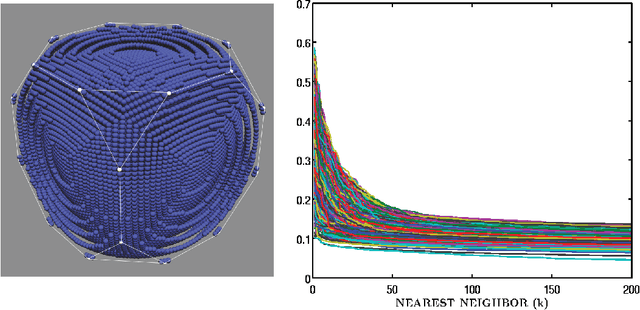
We propose a framework for indexing of grain and sub-grain structures in electron backscatter diffraction (EBSD) images of polycrystalline materials. The framework is based on a previously introduced physics-based forward model by Callahan and De Graef (2013) relating measured patterns to grain orientations (Euler angle). The forward model is tuned to the microscope and the sample symmetry group. We discretize the domain of the forward model onto a dense grid of Euler angles and for each measured pattern we identify the most similar patterns in the dictionary. These patterns are used to identify boundaries, detect anomalies, and index crystal orientations. The statistical distribution of these closest matches is used in an unsupervised binary decision tree (DT) classifier to identify grain boundaries and anomalous regions. The DT classifies a pattern as an anomaly if it has an abnormally low similarity to any pattern in the dictionary. It classifies a pixel as being near a grain boundary if the highly ranked patterns in the dictionary differ significantly over the pixels 3x3 neighborhood. Indexing is accomplished by computing the mean orientation of the closest dictionary matches to each pattern. The mean orientation is estimated using a maximum likelihood approach that models the orientation distribution as a mixture of Von Mises-Fisher distributions over the quaternionic 3-sphere. The proposed dictionary matching approach permits segmentation, anomaly detection, and indexing to be performed in a unified manner with the additional benefit of uncertainty quantification. We demonstrate the proposed dictionary-based approach on a Ni-base IN100 alloy.

Parameter estimation in spherical symmetry groups

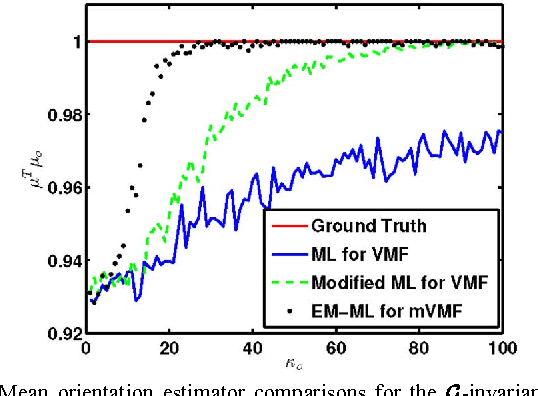
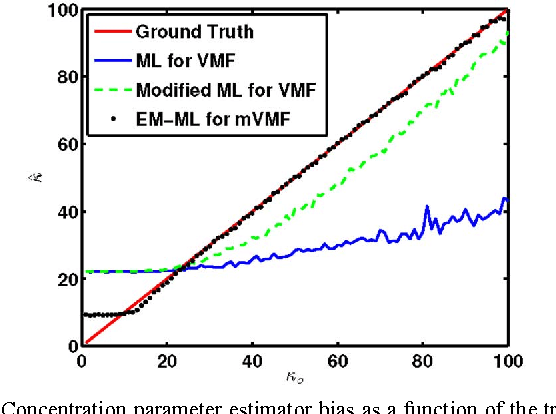
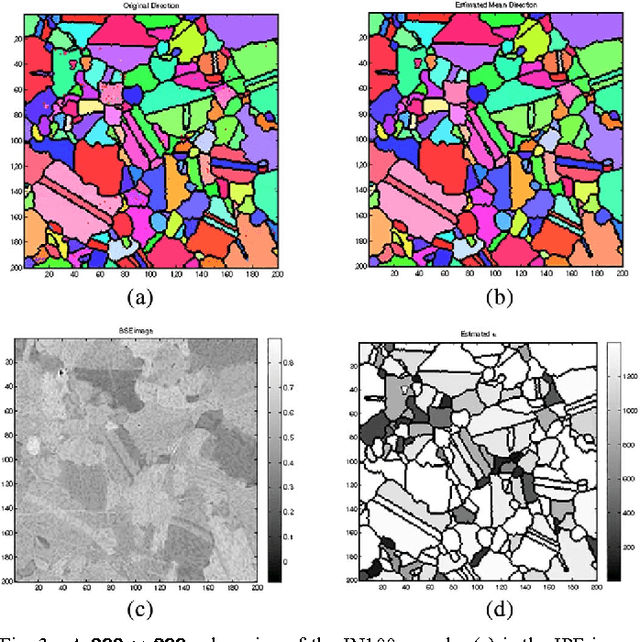
This paper considers statistical estimation problems where the probability distribution of the observed random variable is invariant with respect to actions of a finite topological group. It is shown that any such distribution must satisfy a restricted finite mixture representation. When specialized to the case of distributions over the sphere that are invariant to the actions of a finite spherical symmetry group $\mathcal G$, a group-invariant extension of the Von Mises Fisher (VMF) distribution is obtained. The $\mathcal G$-invariant VMF is parameterized by location and scale parameters that specify the distribution's mean orientation and its concentration about the mean, respectively. Using the restricted finite mixture representation these parameters can be estimated using an Expectation Maximization (EM) maximum likelihood (ML) estimation algorithm. This is illustrated for the problem of mean crystal orientation estimation under the spherically symmetric group associated with the crystal form, e.g., cubic or octahedral or hexahedral. Simulations and experiments establish the advantages of the extended VMF EM-ML estimator for data acquired by Electron Backscatter Diffraction (EBSD) microscopy of a polycrystalline Nickel alloy sample.