Estimation for Compositional Data using Measurements from Nonlinear Systems using Artificial Neural Networks

Our objective is to estimate the unknown compositional input from its output response through an unknown system after estimating the inverse of the original system with a training set. The proposed methods using artificial neural networks (ANNs) can compete with the optimal bounds for linear systems, where convex optimization theory applies, and demonstrate promising results for nonlinear system inversions. We performed extensive experiments by designing numerous different types of nonlinear systems.

A Learning Theory in Linear Systems under Compositional Models

We present a learning theory for the training of a linear system operator having an input compositional variable and propose a Bayesian inversion method for inferring the unknown variable from an output of a noisy linear system. We assume that we have partial or even no knowledge of the operator but have training data of input and ouput. A compositional variable satisfies the constraints that the elements of the variable are all non-negative and sum to unity. We quantified the uncertainty in the trained operator and present the convergence rates of training in explicit forms for several interesting cases under stochastic compositional models. The trained linear operator with the covariance matrix, estimated from the training set of pairs of ground-truth input and noisy output data, is further used in evaluation of posterior uncertainty of the solution. This posterior uncertainty clearly demonstrates uncertainty propagation from noisy training data and addresses possible mismatch between the true operator and the estimated one in the final solution.

A Dictionary Approach to EBSD Indexing

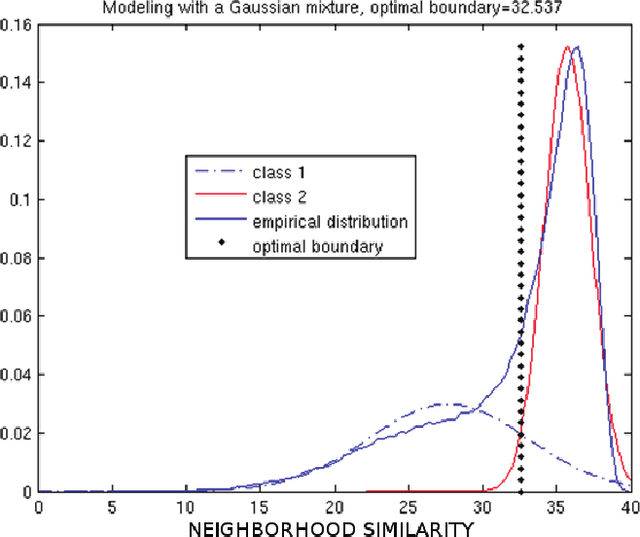
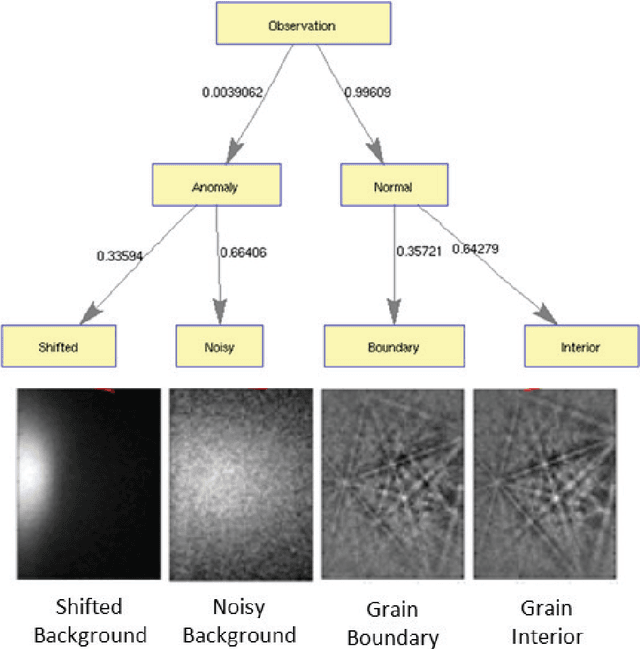
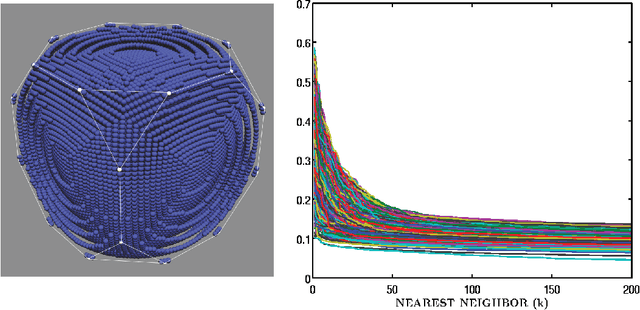
We propose a framework for indexing of grain and sub-grain structures in electron backscatter diffraction (EBSD) images of polycrystalline materials. The framework is based on a previously introduced physics-based forward model by Callahan and De Graef (2013) relating measured patterns to grain orientations (Euler angle). The forward model is tuned to the microscope and the sample symmetry group. We discretize the domain of the forward model onto a dense grid of Euler angles and for each measured pattern we identify the most similar patterns in the dictionary. These patterns are used to identify boundaries, detect anomalies, and index crystal orientations. The statistical distribution of these closest matches is used in an unsupervised binary decision tree (DT) classifier to identify grain boundaries and anomalous regions. The DT classifies a pattern as an anomaly if it has an abnormally low similarity to any pattern in the dictionary. It classifies a pixel as being near a grain boundary if the highly ranked patterns in the dictionary differ significantly over the pixels 3x3 neighborhood. Indexing is accomplished by computing the mean orientation of the closest dictionary matches to each pattern. The mean orientation is estimated using a maximum likelihood approach that models the orientation distribution as a mixture of Von Mises-Fisher distributions over the quaternionic 3-sphere. The proposed dictionary matching approach permits segmentation, anomaly detection, and indexing to be performed in a unified manner with the additional benefit of uncertainty quantification. We demonstrate the proposed dictionary-based approach on a Ni-base IN100 alloy.

Variational Semi-blind Sparse Deconvolution with Orthogonal Kernel Bases and its Application to MRFM

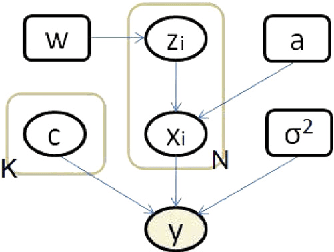
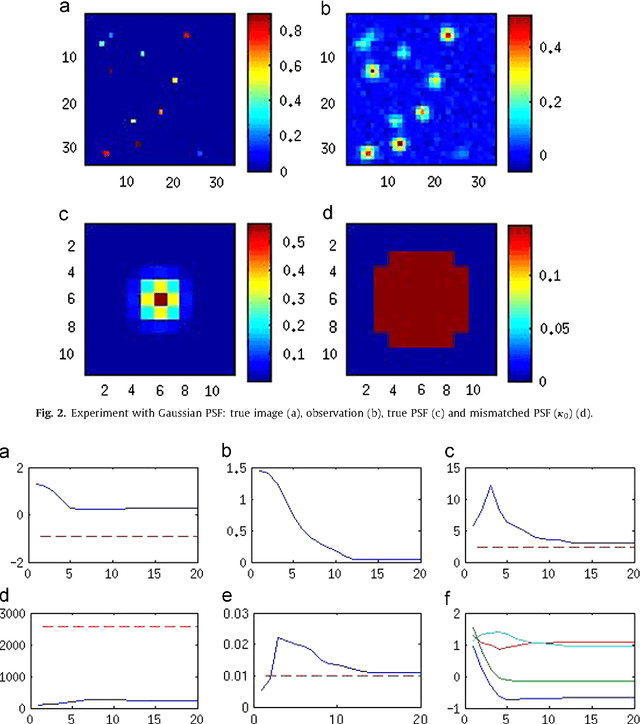
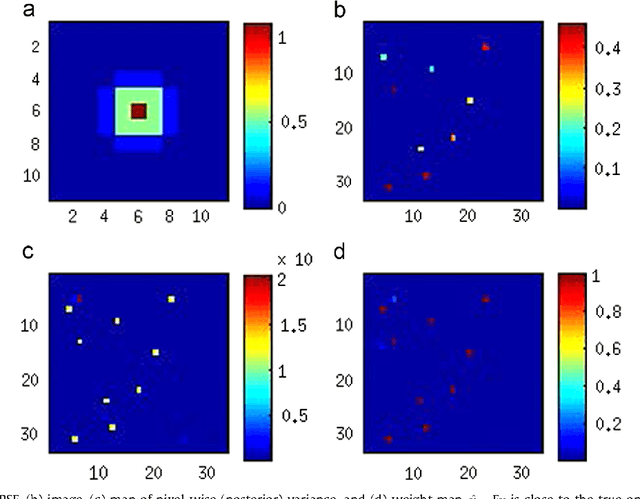
We present a variational Bayesian method of joint image reconstruction and point spread function (PSF) estimation when the PSF of the imaging device is only partially known. To solve this semi-blind deconvolution problem, prior distributions are specified for the PSF and the 3D image. Joint image reconstruction and PSF estimation is then performed within a Bayesian framework, using a variational algorithm to estimate the posterior distribution. The image prior distribution imposes an explicit atomic measure that corresponds to image sparsity. Importantly, the proposed Bayesian deconvolution algorithm does not require hand tuning. Simulation results clearly demonstrate that the semi-blind deconvolution algorithm compares favorably with previous Markov chain Monte Carlo (MCMC) version of myopic sparse reconstruction. It significantly outperforms mismatched non-blind algorithms that rely on the assumption of the perfect knowledge of the PSF. The algorithm is illustrated on real data from magnetic resonance force microscopy (MRFM).

Semi-blind Sparse Image Reconstruction with Application to MRFM

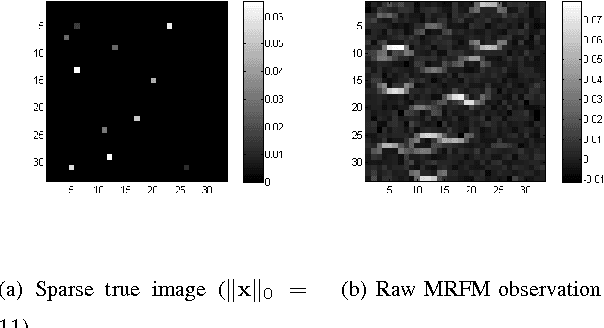
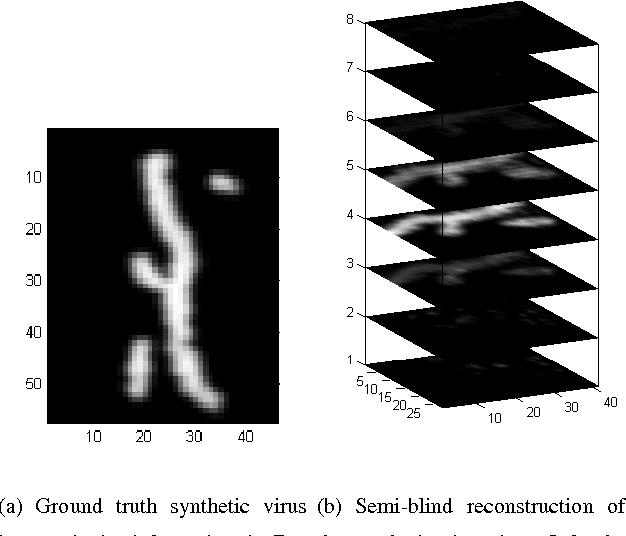
We propose a solution to the image deconvolution problem where the convolution kernel or point spread function (PSF) is assumed to be only partially known. Small perturbations generated from the model are exploited to produce a few principal components explaining the PSF uncertainty in a high dimensional space. Unlike recent developments on blind deconvolution of natural images, we assume the image is sparse in the pixel basis, a natural sparsity arising in magnetic resonance force microscopy (MRFM). Our approach adopts a Bayesian Metropolis-within-Gibbs sampling framework. The performance of our Bayesian semi-blind algorithm for sparse images is superior to previously proposed semi-blind algorithms such as the alternating minimization (AM) algorithm and blind algorithms developed for natural images. We illustrate our myopic algorithm on real MRFM tobacco virus data.