Rethinking Structure Learning For Graph Neural Networks

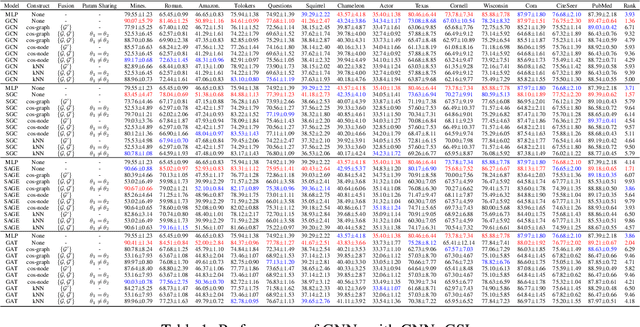
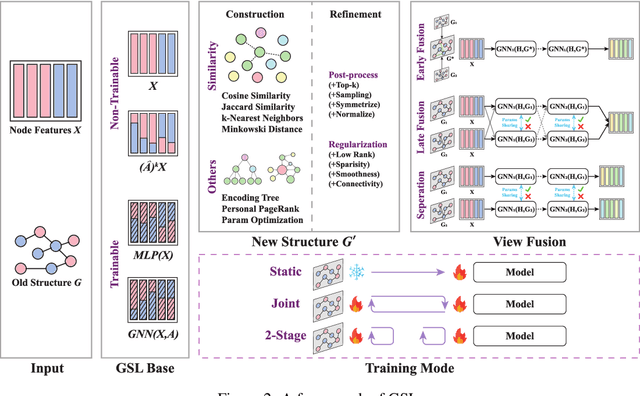
To improve the performance of Graph Neural Networks (GNNs), Graph Structure Learning (GSL) has been extensively applied to reconstruct or refine original graph structures, effectively addressing issues like heterophily, over-squashing, and noisy structures. While GSL is generally thought to improve GNN performance, it often leads to longer training times and more hyperparameter tuning. Besides, the distinctions among current GSL methods remain ambiguous from the perspective of GNN training, and there is a lack of theoretical analysis to quantify their effectiveness. Recent studies further suggest that, under fair comparisons with the same hyperparameter tuning, GSL does not consistently outperform baseline GNNs. This motivates us to ask a critical question: is GSL really useful for GNNs? To address this question, this paper makes two key contributions. First, we propose a new GSL framework, which includes three steps: GSL base (the representation used for GSL) construction, new structure construction, and view fusion, to better understand the effectiveness of GSL in GNNs. Second, after graph convolution, we analyze the differences in mutual information (MI) between node representations derived from the original topology and those from the newly constructed topology. Surprisingly, our empirical observations and theoretical analysis show that no matter which type of graph structure construction methods are used, after feeding the same GSL bases to the newly constructed graph, there is no MI gain compared to the original GSL bases. To fairly reassess the effectiveness of GSL, we conduct ablation experiments and find that it is the pretrained GSL bases that enhance GNN performance, and in most cases, GSL cannot improve GNN performance. This finding encourages us to rethink the essential components in GNNs, such as self-training and structural encoding, in GNN design rather than GSL.

Is Graph Convolution Always Beneficial For Every Feature?

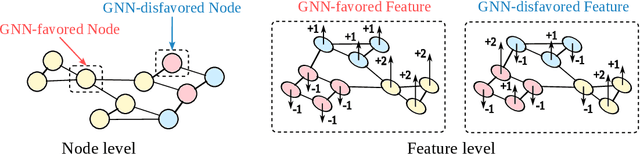
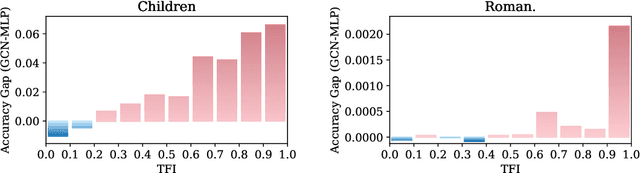
Graph Neural Networks (GNNs) have demonstrated strong capabilities in processing structured data. While traditional GNNs typically treat each feature dimension equally during graph convolution, we raise an important question: Is the graph convolution operation equally beneficial for each feature? If not, the convolution operation on certain feature dimensions can possibly lead to harmful effects, even worse than the convolution-free models. In prior studies, to assess the impacts of graph convolution on features, people proposed metrics based on feature homophily to measure feature consistency with the graph topology. However, these metrics have shown unsatisfactory alignment with GNN performance and have not been effectively employed to guide feature selection in GNNs. To address these limitations, we introduce a novel metric, Topological Feature Informativeness (TFI), to distinguish between GNN-favored and GNN-disfavored features, where its effectiveness is validated through both theoretical analysis and empirical observations. Based on TFI, we propose a simple yet effective Graph Feature Selection (GFS) method, which processes GNN-favored and GNN-disfavored features separately, using GNNs and non-GNN models. Compared to original GNNs, GFS significantly improves the extraction of useful topological information from each feature with comparable computational costs. Extensive experiments show that after applying GFS to 8 baseline and state-of-the-art (SOTA) GNN architectures across 10 datasets, 83.75% of the GFS-augmented cases show significant performance boosts. Furthermore, our proposed TFI metric outperforms other feature selection methods. These results validate the effectiveness of both GFS and TFI. Additionally, we demonstrate that GFS's improvements are robust to hyperparameter tuning, highlighting its potential as a universal method for enhancing various GNN architectures.

What Is Missing In Homophily? Disentangling Graph Homophily For Graph Neural Networks

Graph homophily refers to the phenomenon that connected nodes tend to share similar characteristics. Understanding this concept and its related metrics is crucial for designing effective Graph Neural Networks (GNNs). The most widely used homophily metrics, such as edge or node homophily, quantify such "similarity" as label consistency across the graph topology. These metrics are believed to be able to reflect the performance of GNNs, especially on node-level tasks. However, many recent studies have empirically demonstrated that the performance of GNNs does not always align with homophily metrics, and how homophily influences GNNs still remains unclear and controversial. Then, a crucial question arises: What is missing in our current understanding of homophily? To figure out the missing part, in this paper, we disentangle the graph homophily into $3$ aspects: label, structural, and feature homophily, providing a more comprehensive understanding of GNN performance. To investigate their synergy, we propose a Contextual Stochastic Block Model with $3$ types of Homophily (CSBM-3H), where the topology and feature generation are controlled by the $3$ metrics. Based on the theoretical analysis of CSBM-3H, we derive a new composite metric, named Tri-Hom, that considers all $3$ aspects and overcomes the limitations of conventional homophily metrics. The theoretical conclusions and the effectiveness of Tri-Hom have been verified through synthetic experiments on CSBM-3H. In addition, we conduct experiments on $31$ real-world benchmark datasets and calculate the correlations between homophily metrics and model performance. Tri-Hom has significantly higher correlation values than $17$ existing metrics that only focus on a single homophily aspect, demonstrating its superiority and the importance of homophily synergy. Our code is available at \url{https://github.com/zylMozart/Disentangle_GraphHom}.

Learn from Heterophily: Heterophilous Information-enhanced Graph Neural Network

Under circumstances of heterophily, where nodes with different labels tend to be connected based on semantic meanings, Graph Neural Networks (GNNs) often exhibit suboptimal performance. Current studies on graph heterophily mainly focus on aggregation calibration or neighbor extension and address the heterophily issue by utilizing node features or structural information to improve GNN representations. In this paper, we propose and demonstrate that the valuable semantic information inherent in heterophily can be utilized effectively in graph learning by investigating the distribution of neighbors for each individual node within the graph. The theoretical analysis is carried out to demonstrate the efficacy of the idea in enhancing graph learning. Based on this analysis, we propose HiGNN, an innovative approach that constructs an additional new graph structure, that integrates heterophilous information by leveraging node distribution to enhance connectivity between nodes that share similar semantic characteristics. We conduct empirical assessments on node classification tasks using both homophilous and heterophilous benchmark datasets and compare HiGNN to popular GNN baselines and SoTA methods, confirming the effectiveness in improving graph representations. In addition, by incorporating heterophilous information, we demonstrate a notable enhancement in existing GNN-based approaches, and the homophily degree across real-world datasets, thus affirming the efficacy of our approach.