Multi-User Chat Assistant : a Framework Using LLMs to Facilitate Group Conversations

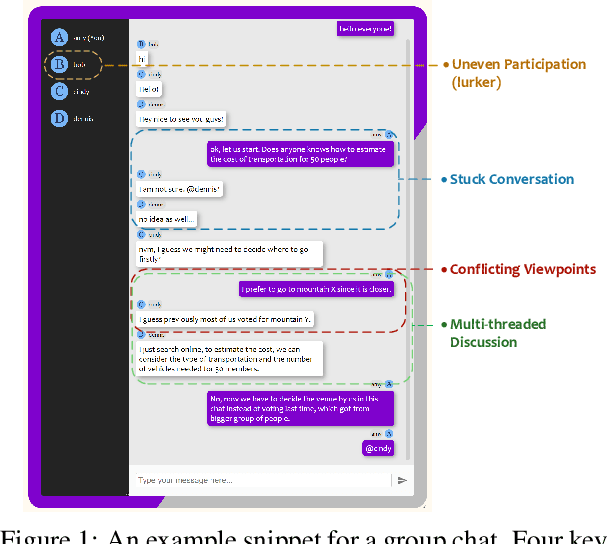
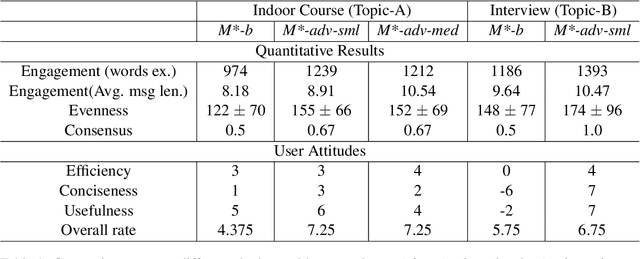
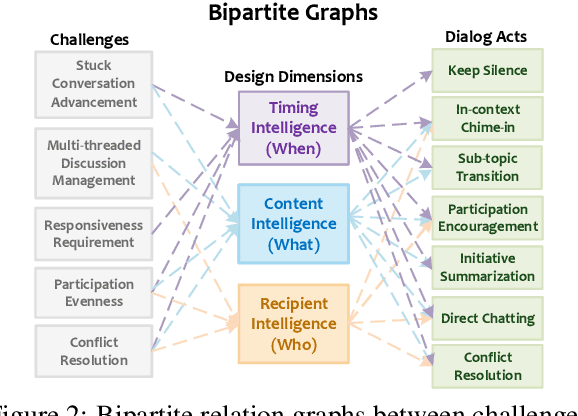
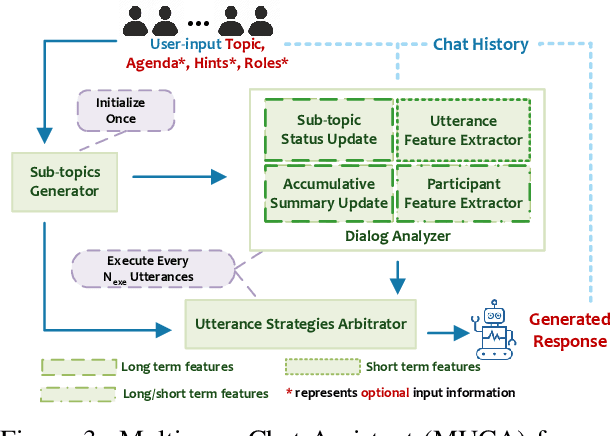
Recent advancements in large language models (LLMs) have provided a new avenue for chatbot development, while most existing research has primarily centered on single-user chatbots that focus on deciding "What" to answer after user inputs. In this paper, we identified that multi-user chatbots have more complex 3W design dimensions -- "What" to say, "When" to respond, and "Who" to answer. Additionally, we proposed Multi-User Chat Assistant (MUCA), which is an LLM-based framework for chatbots specifically designed for group discussions. MUCA consists of three main modules: Sub-topic Generator, Dialog Analyzer, and Utterance Strategies Arbitrator. These modules jointly determine suitable response contents, timings, and the appropriate recipients. To make the optimizing process for MUCA easier, we further propose an LLM-based Multi-User Simulator (MUS) that can mimic real user behavior. This enables faster simulation of a conversation between the chatbot and simulated users, making the early development of the chatbot framework much more efficient. MUCA demonstrates effectiveness, including appropriate chime-in timing, relevant content, and positive user engagement, in goal-oriented conversations with a small to medium number of participants, as evidenced by case studies and experimental results from user studies.

KerGM: Kernelized Graph Matching

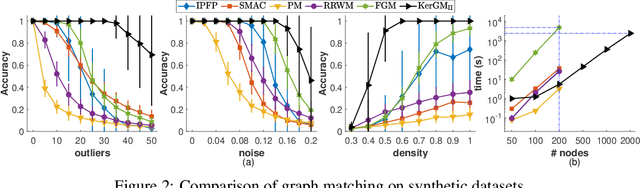
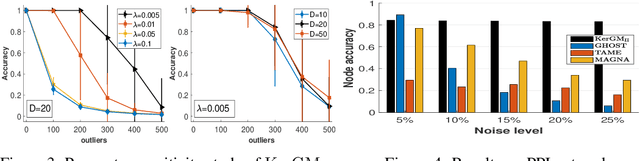
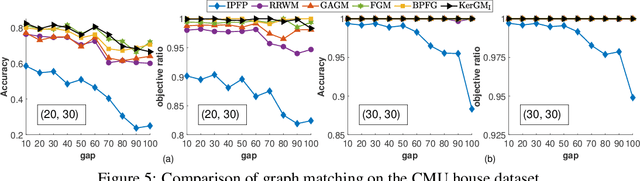
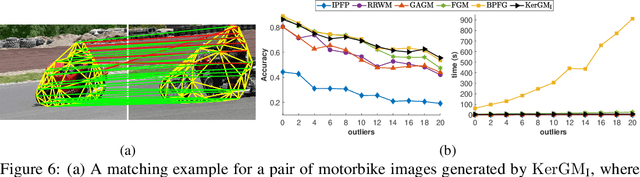
Graph matching plays a central role in such fields as computer vision, pattern recognition, and bioinformatics. Graph matching problems can be cast as two types of quadratic assignment problems (QAPs): Koopmans-Beckmann's QAP or Lawler's QAP. In our paper, we provide a unifying view for these two problems by introducing new rules for array operations in Hilbert spaces. Consequently, Lawler's QAP can be considered as the Koopmans-Beckmann's alignment between two arrays in reproducing kernel Hilbert spaces (RKHS), making it possible to efficiently solve the problem without computing a huge affinity matrix. Furthermore, we develop the entropy-regularized Frank-Wolfe (EnFW) algorithm for optimizing QAPs, which has the same convergence rate as the original FW algorithm while dramatically reducing the computational burden for each outer iteration. We conduct extensive experiments to evaluate our approach, and show that our algorithm significantly outperforms the state-of-the-art in both matching accuracy and scalability.

RetGK: Graph Kernels based on Return Probabilities of Random Walks

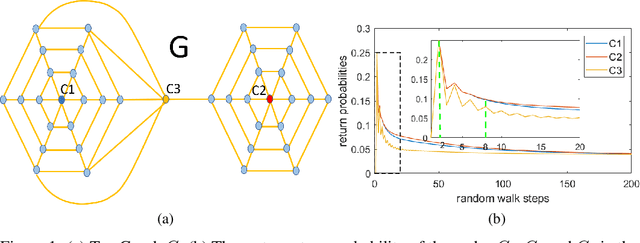
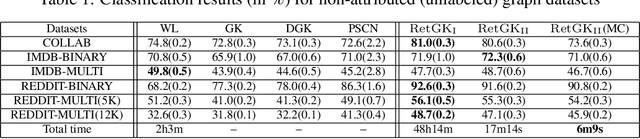
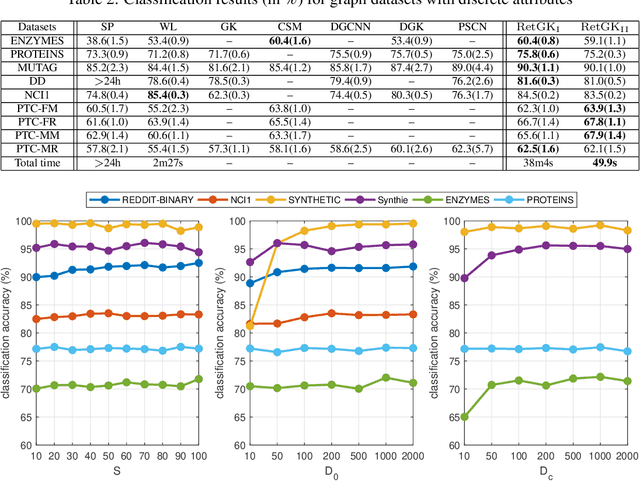
Graph-structured data arise in wide applications, such as computer vision, bioinformatics, and social networks. Quantifying similarities among graphs is a fundamental problem. In this paper, we develop a framework for computing graph kernels, based on return probabilities of random walks. The advantages of our proposed kernels are that they can effectively exploit various node attributes, while being scalable to large datasets. We conduct extensive graph classification experiments to evaluate our graph kernels. The experimental results show that our graph kernels significantly outperform existing state-of-the-art approaches in both accuracy and computational efficiency.