KerGM: Kernelized Graph Matching
Paper and Code
Nov 25, 2019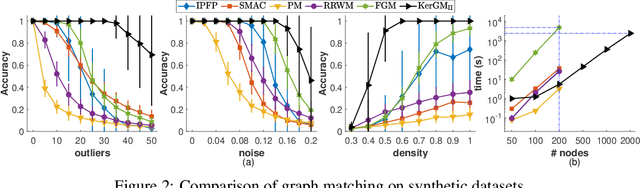
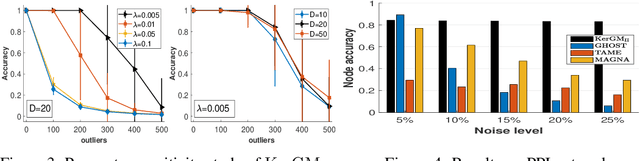
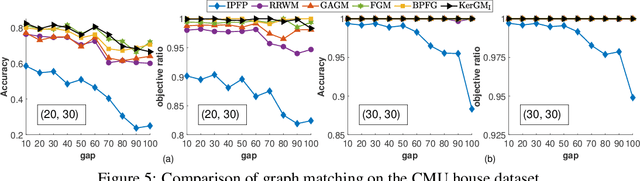
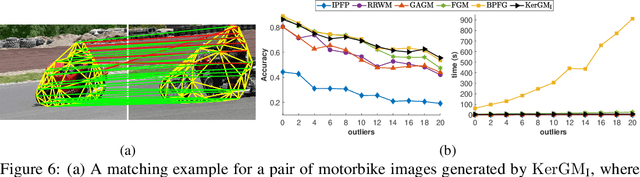
Graph matching plays a central role in such fields as computer vision, pattern recognition, and bioinformatics. Graph matching problems can be cast as two types of quadratic assignment problems (QAPs): Koopmans-Beckmann's QAP or Lawler's QAP. In our paper, we provide a unifying view for these two problems by introducing new rules for array operations in Hilbert spaces. Consequently, Lawler's QAP can be considered as the Koopmans-Beckmann's alignment between two arrays in reproducing kernel Hilbert spaces (RKHS), making it possible to efficiently solve the problem without computing a huge affinity matrix. Furthermore, we develop the entropy-regularized Frank-Wolfe (EnFW) algorithm for optimizing QAPs, which has the same convergence rate as the original FW algorithm while dramatically reducing the computational burden for each outer iteration. We conduct extensive experiments to evaluate our approach, and show that our algorithm significantly outperforms the state-of-the-art in both matching accuracy and scalability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge