Estimating uterine activity from electrohysterogram measurements via statistical tensor decomposition

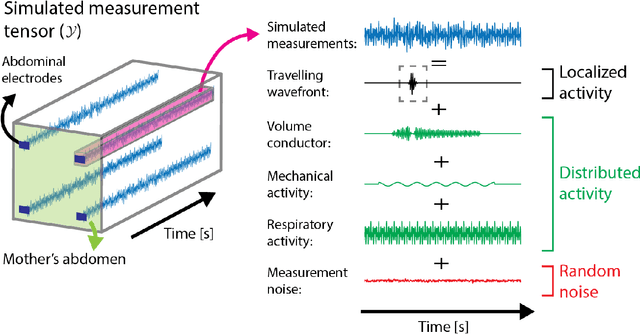
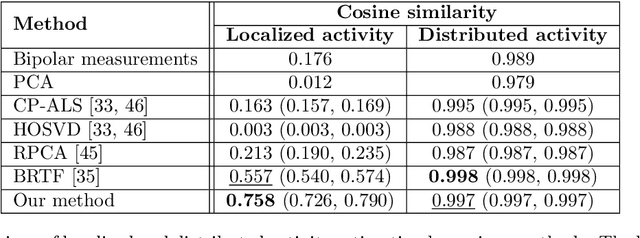
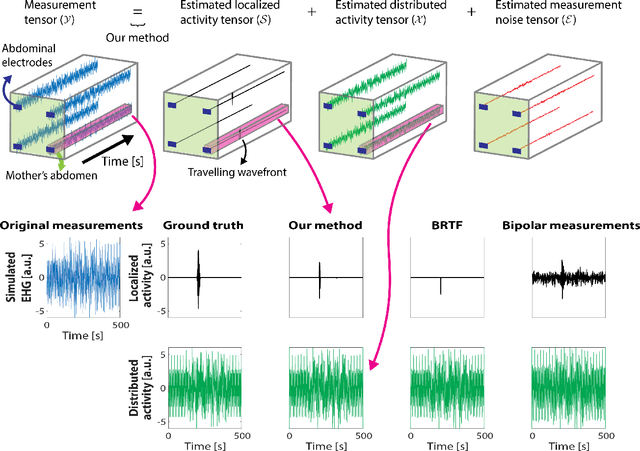
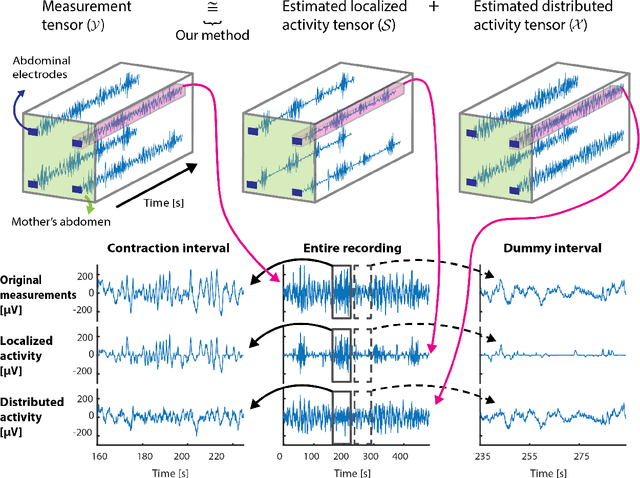
Complications during pregnancy and labor are frequent and are especially damaging in populations with limited access to healthcare. To mitigate these complications, electrohysterograms (EHG), which measure abdominal electric potentials noninvasively, have been proposed for monitoring uterine activity. However, EHGs record electrical activity from sources besides the uterus, complicating their analysis. Here, we represent multi-electrode EHG measurements as tensors and develop a Bayesian tensor decomposition for estimating localized and distributed electrical activities. Using simulated measurements, we demonstrate that our method can estimate localized and distributed activities more accurately than other methods, achieving cosine similarities with the ground truth of 0.758 (95% confidence interval (CI): 0.726-0.790) and 0.997 (95% CI: 0.997-0.997), respectively. Using real measurements, we show the advantages of our method for separating uterine electrical activity during contractions from other electrical activities measured in EHGs, achieving averaged signal-to-noise ratios of 7.36 (95% CI: 6.70-8.02) and 9.05 (95% CI: 8.24-9.86) dB in two datasets. Such accurate estimation of uterine activity from EHG measurements could be useful in developing reliable future applications, implemented in portable devices, to reduce risks during pregnancy and labor.

KerGM: Kernelized Graph Matching

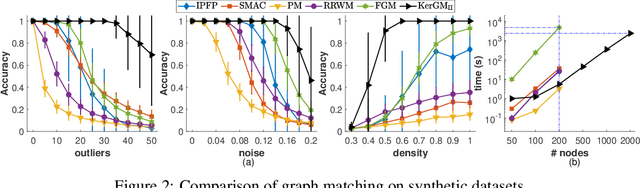
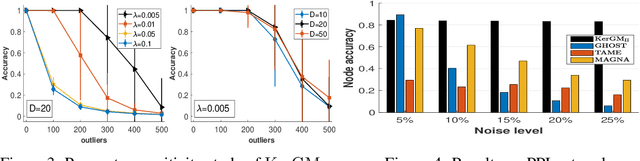
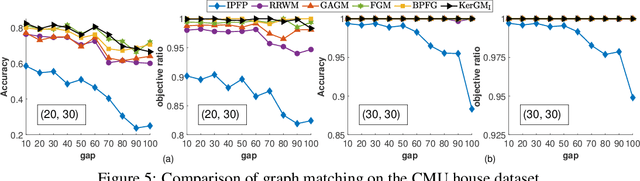
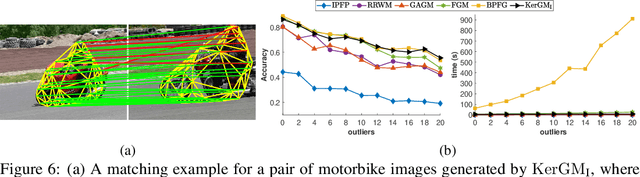
Graph matching plays a central role in such fields as computer vision, pattern recognition, and bioinformatics. Graph matching problems can be cast as two types of quadratic assignment problems (QAPs): Koopmans-Beckmann's QAP or Lawler's QAP. In our paper, we provide a unifying view for these two problems by introducing new rules for array operations in Hilbert spaces. Consequently, Lawler's QAP can be considered as the Koopmans-Beckmann's alignment between two arrays in reproducing kernel Hilbert spaces (RKHS), making it possible to efficiently solve the problem without computing a huge affinity matrix. Furthermore, we develop the entropy-regularized Frank-Wolfe (EnFW) algorithm for optimizing QAPs, which has the same convergence rate as the original FW algorithm while dramatically reducing the computational burden for each outer iteration. We conduct extensive experiments to evaluate our approach, and show that our algorithm significantly outperforms the state-of-the-art in both matching accuracy and scalability.

RetGK: Graph Kernels based on Return Probabilities of Random Walks

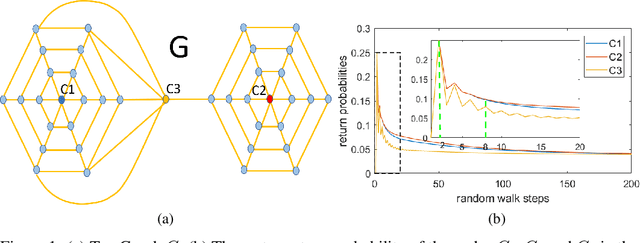
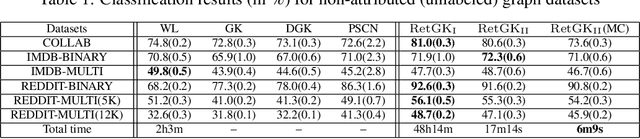
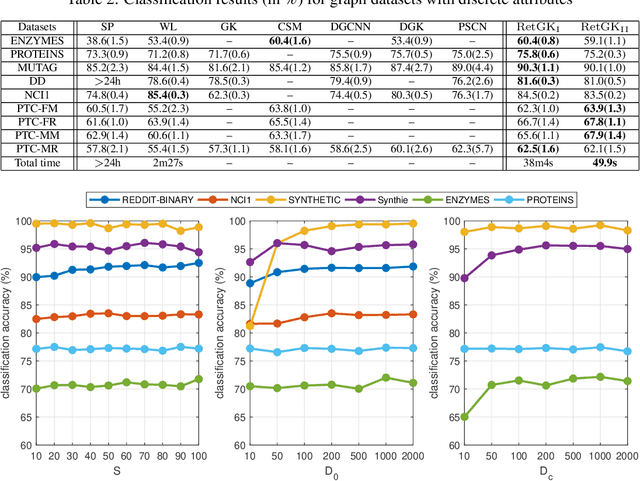
Graph-structured data arise in wide applications, such as computer vision, bioinformatics, and social networks. Quantifying similarities among graphs is a fundamental problem. In this paper, we develop a framework for computing graph kernels, based on return probabilities of random walks. The advantages of our proposed kernels are that they can effectively exploit various node attributes, while being scalable to large datasets. We conduct extensive graph classification experiments to evaluate our graph kernels. The experimental results show that our graph kernels significantly outperform existing state-of-the-art approaches in both accuracy and computational efficiency.

GPatt: Fast Multidimensional Pattern Extrapolation with Gaussian Processes

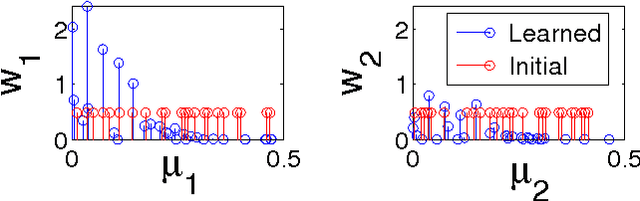
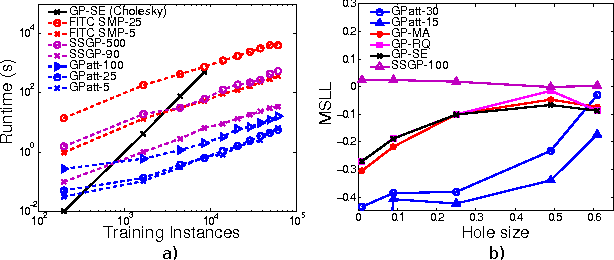
Gaussian processes are typically used for smoothing and interpolation on small datasets. We introduce a new Bayesian nonparametric framework -- GPatt -- enabling automatic pattern extrapolation with Gaussian processes on large multidimensional datasets. GPatt unifies and extends highly expressive kernels and fast exact inference techniques. Without human intervention -- no hand crafting of kernel features, and no sophisticated initialisation procedures -- we show that GPatt can solve large scale pattern extrapolation, inpainting, and kernel discovery problems, including a problem with 383400 training points. We find that GPatt significantly outperforms popular alternative scalable Gaussian process methods in speed and accuracy. Moreover, we discover profound differences between each of these methods, suggesting expressive kernels, nonparametric representations, and exact inference are useful for modelling large scale multidimensional patterns.