Unit Commitment using Nearest Neighbor as a Short-Term Proxy

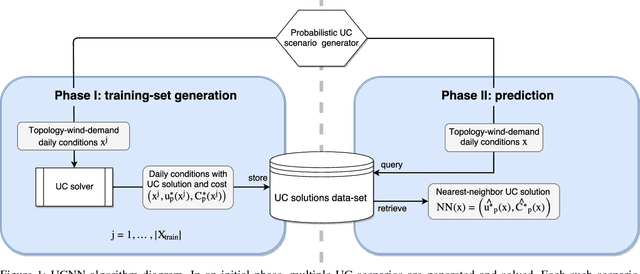
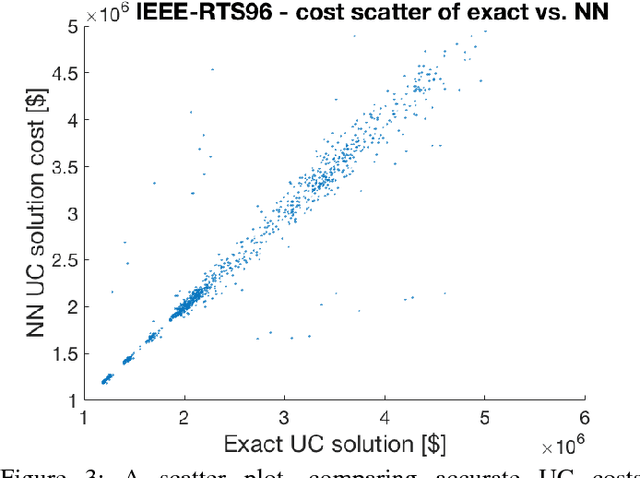
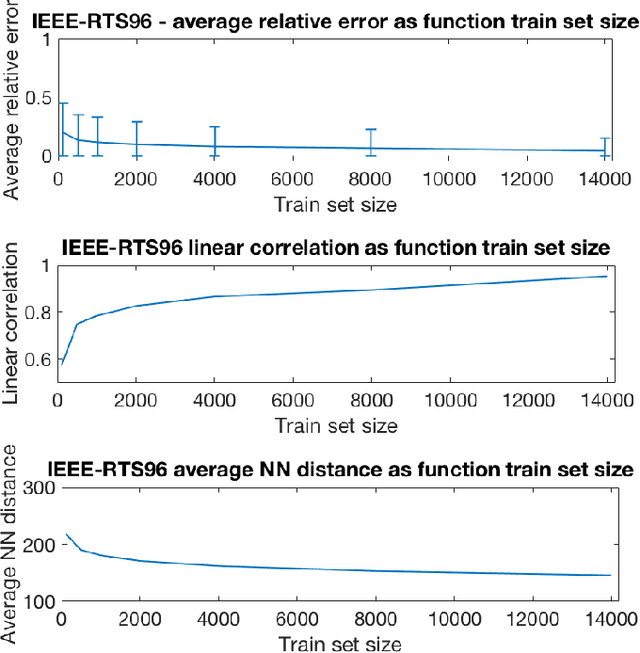
We devise the Unit Commitment Nearest Neighbor (UCNN) algorithm to be used as a proxy for quickly approximating outcomes of short-term decisions, to make tractable hierarchical long-term assessment and planning for large power systems. Experimental results on updated versions of IEEE-RTS79 and IEEE-RTS96 show high accuracy measured on operational cost, achieved in runtimes that are lower in several orders of magnitude than the traditional approach.

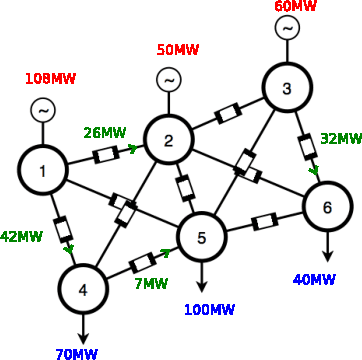
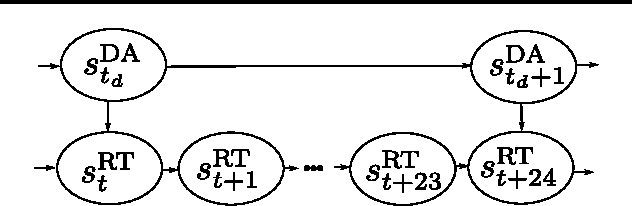
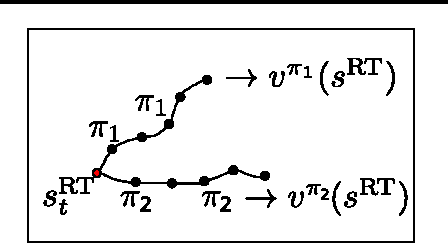
Hierarchical Decision Making In Electricity Grid Management

The power grid is a complex and vital system that necessitates careful reliability management. Managing the grid is a difficult problem with multiple time scales of decision making and stochastic behavior due to renewable energy generations, variable demand and unplanned outages. Solving this problem in the face of uncertainty requires a new methodology with tractable algorithms. In this work, we introduce a new model for hierarchical decision making in complex systems. We apply reinforcement learning (RL) methods to learn a proxy, i.e., a level of abstraction, for real-time power grid reliability. We devise an algorithm that alternates between slow time-scale policy improvement, and fast time-scale value function approximation. We compare our results to prevailing heuristics, and show the strength of our method.

GPatt: Fast Multidimensional Pattern Extrapolation with Gaussian Processes

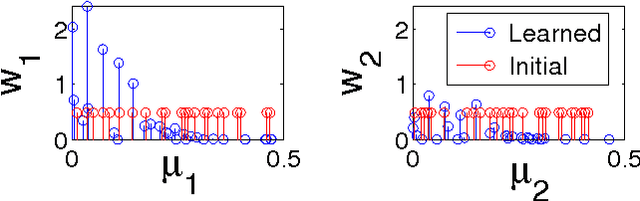
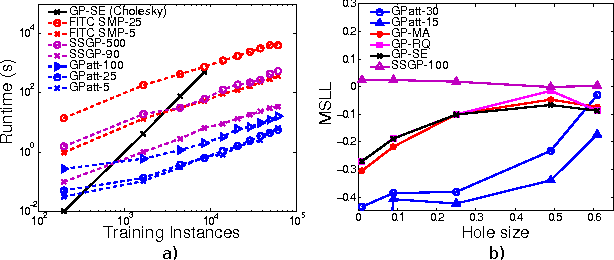
Gaussian processes are typically used for smoothing and interpolation on small datasets. We introduce a new Bayesian nonparametric framework -- GPatt -- enabling automatic pattern extrapolation with Gaussian processes on large multidimensional datasets. GPatt unifies and extends highly expressive kernels and fast exact inference techniques. Without human intervention -- no hand crafting of kernel features, and no sophisticated initialisation procedures -- we show that GPatt can solve large scale pattern extrapolation, inpainting, and kernel discovery problems, including a problem with 383400 training points. We find that GPatt significantly outperforms popular alternative scalable Gaussian process methods in speed and accuracy. Moreover, we discover profound differences between each of these methods, suggesting expressive kernels, nonparametric representations, and exact inference are useful for modelling large scale multidimensional patterns.

Scaling Multidimensional Inference for Structured Gaussian Processes

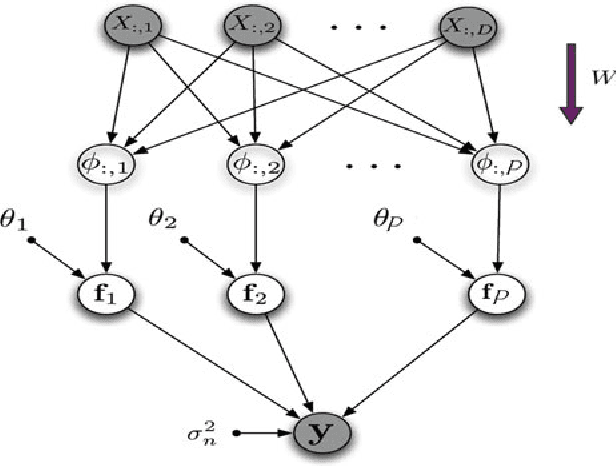
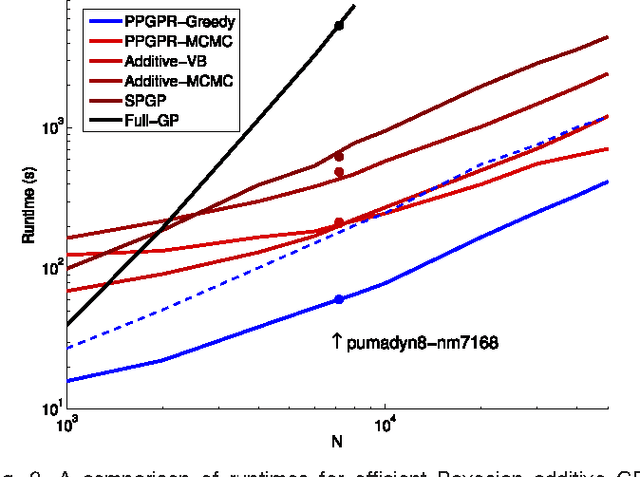
Exact Gaussian Process (GP) regression has O(N^3) runtime for data size N, making it intractable for large N. Many algorithms for improving GP scaling approximate the covariance with lower rank matrices. Other work has exploited structure inherent in particular covariance functions, including GPs with implied Markov structure, and equispaced inputs (both enable O(N) runtime). However, these GP advances have not been extended to the multidimensional input setting, despite the preponderance of multidimensional applications. This paper introduces and tests novel extensions of structured GPs to multidimensional inputs. We present new methods for additive GPs, showing a novel connection between the classic backfitting method and the Bayesian framework. To achieve optimal accuracy-complexity tradeoff, we extend this model with a novel variant of projection pursuit regression. Our primary result -- projection pursuit Gaussian Process Regression -- shows orders of magnitude speedup while preserving high accuracy. The natural second and third steps include non-Gaussian observations and higher dimensional equispaced grid methods. We introduce novel techniques to address both of these necessary directions. We thoroughly illustrate the power of these three advances on several datasets, achieving close performance to the naive Full GP at orders of magnitude less cost.