Yunus Saatçi
Scaling Multidimensional Inference for Structured Gaussian Processes
Sep 21, 2012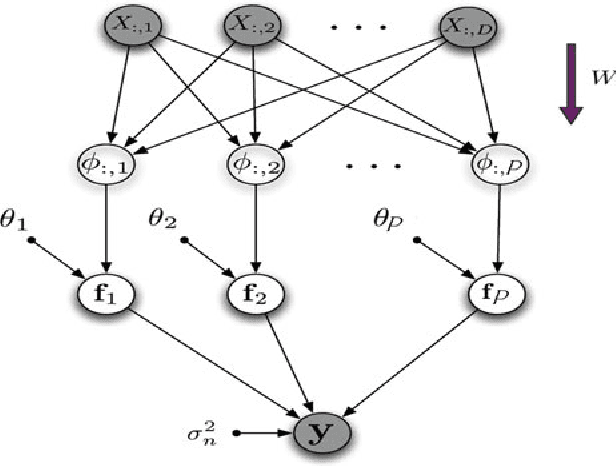

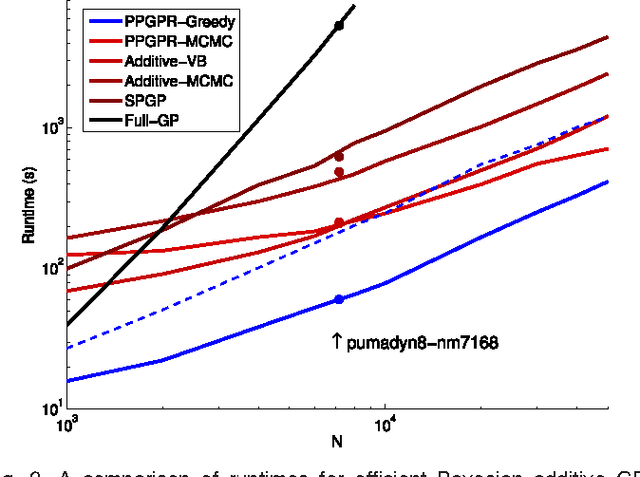

Abstract:Exact Gaussian Process (GP) regression has O(N^3) runtime for data size N, making it intractable for large N. Many algorithms for improving GP scaling approximate the covariance with lower rank matrices. Other work has exploited structure inherent in particular covariance functions, including GPs with implied Markov structure, and equispaced inputs (both enable O(N) runtime). However, these GP advances have not been extended to the multidimensional input setting, despite the preponderance of multidimensional applications. This paper introduces and tests novel extensions of structured GPs to multidimensional inputs. We present new methods for additive GPs, showing a novel connection between the classic backfitting method and the Bayesian framework. To achieve optimal accuracy-complexity tradeoff, we extend this model with a novel variant of projection pursuit regression. Our primary result -- projection pursuit Gaussian Process Regression -- shows orders of magnitude speedup while preserving high accuracy. The natural second and third steps include non-Gaussian observations and higher dimensional equispaced grid methods. We introduce novel techniques to address both of these necessary directions. We thoroughly illustrate the power of these three advances on several datasets, achieving close performance to the naive Full GP at orders of magnitude less cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge