A Privacy-Preserving Framework for Advertising Personalization Incorporating Federated Learning and Differential Privacy

To mitigate privacy leakage and performance issues in personalized advertising, this paper proposes a framework that integrates federated learning and differential privacy. The system combines distributed feature extraction, dynamic privacy budget allocation, and robust model aggregation to balance model accuracy, communication overhead, and privacy protection. Multi-party secure computing and anomaly detection mechanisms further enhance system resilience against malicious attacks. Experimental results demonstrate that the framework achieves dual optimization of recommendation accuracy and system efficiency while ensuring privacy, providing both a practical solution and a theoretical foundation for applying privacy protection technologies in advertisement recommendation.

Liner Shipping Network Design with Reinforcement Learning

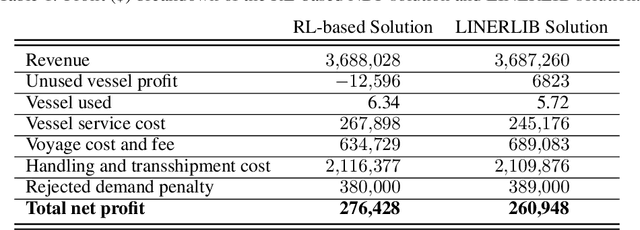
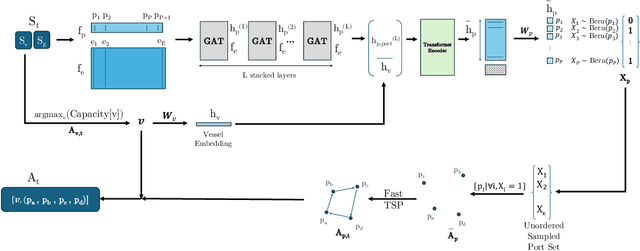
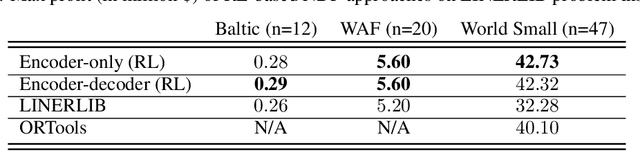
This paper proposes a novel reinforcement learning framework to address the Liner Shipping Network Design Problem (LSNDP), a challenging combinatorial optimization problem focused on designing cost-efficient maritime shipping routes. Traditional methods for solving the LSNDP typically involve decomposing the problem into sub-problems, such as network design and multi-commodity flow, which are then tackled using approximate heuristics or large neighborhood search (LNS) techniques. In contrast, our approach employs a model-free reinforcement learning algorithm on the network design, integrated with a heuristic-based multi-commodity flow solver, to produce competitive results on the publicly available LINERLIB benchmark. Additionally, our method also demonstrates generalization capabilities by producing competitive solutions on the benchmark instances after training on perturbed instances.

Time-Optimal Planning for Long-Range Quadrotor Flights: An Automatic Optimal Synthesis Approach

Time-critical tasks such as drone racing typically cover large operation areas. However, it is difficult and computationally intensive for current time-optimal motion planners to accommodate long flight distances since a large yet unknown number of knot points is required to represent the trajectory. We present a polynomial-based automatic optimal synthesis (AOS) approach that can address this challenge. Our method not only achieves superior time optimality but also maintains a consistently low computational cost across different ranges while considering the full quadrotor dynamics. First, we analyze the properties of time-optimal quadrotor maneuvers to determine the minimal number of polynomial pieces required to capture the dominant structure of time-optimal trajectories. This enables us to represent substantially long minimum-time trajectories with a minimal set of variables. Then, a robust optimization scheme is developed to handle arbitrary start and end conditions as well as intermediate waypoints. Extensive comparisons show that our approach is faster than the state-of-the-art approach by orders of magnitude with comparable time optimality. Real-world experiments further validate the quality of the resulting trajectories, demonstrating aggressive time-optimal maneuvers with a peak velocity of 8.86 m/s.

Reusing Historical Trajectories in Natural Policy Gradient via Importance Sampling: Convergence and Convergence Rate

Reinforcement learning provides a mathematical framework for learning-based control, whose success largely depends on the amount of data it can utilize. The efficient utilization of historical trajectories obtained from previous policies is essential for expediting policy optimization. Empirical evidence has shown that policy gradient methods based on importance sampling work well. However, existing literature often neglect the interdependence between trajectories from different iterations, and the good empirical performance lacks a rigorous theoretical justification. In this paper, we study a variant of the natural policy gradient method with reusing historical trajectories via importance sampling. We show that the bias of the proposed estimator of the gradient is asymptotically negligible, the resultant algorithm is convergent, and reusing past trajectories helps improve the convergence rate. We further apply the proposed estimator to popular policy optimization algorithms such as trust region policy optimization. Our theoretical results are verified on classical benchmarks.

Risk-averse Contextual Multi-armed Bandit Problem with Linear Payoffs

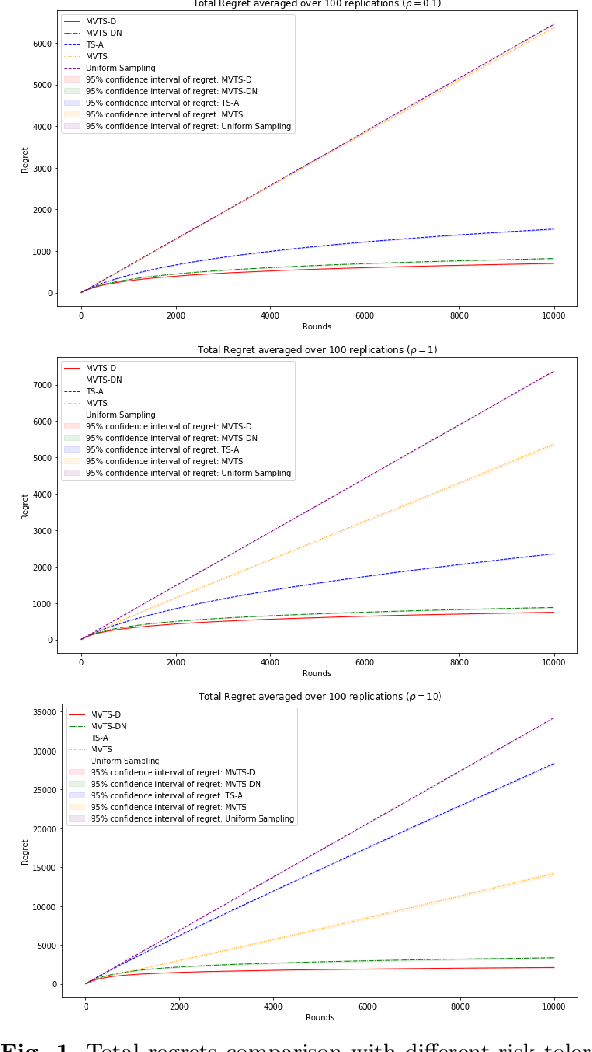
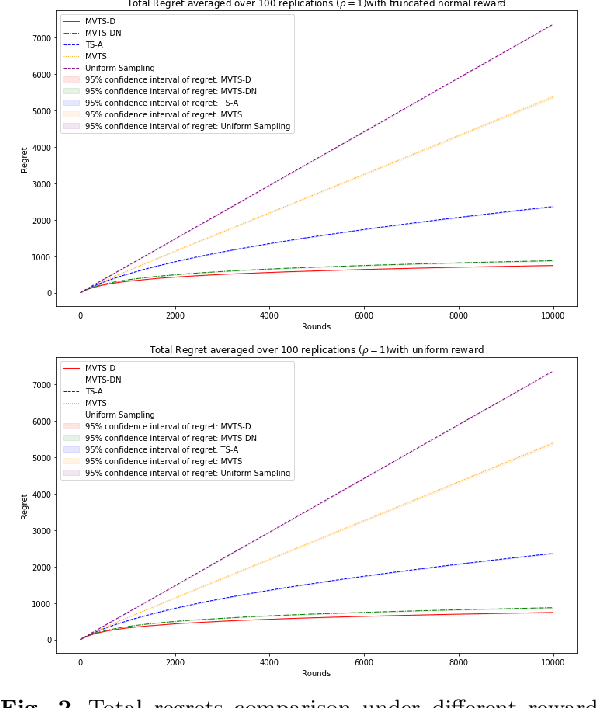
In this paper we consider the contextual multi-armed bandit problem for linear payoffs under a risk-averse criterion. At each round, contexts are revealed for each arm, and the decision maker chooses one arm to pull and receives the corresponding reward. In particular, we consider mean-variance as the risk criterion, and the best arm is the one with the largest mean-variance reward. We apply the Thompson Sampling algorithm for the disjoint model, and provide a comprehensive regret analysis for a variant of the proposed algorithm. For $T$ rounds, $K$ actions, and $d$-dimensional feature vectors, we prove a regret bound of $O((1+\rho+\frac{1}{\rho}) d\ln T \ln \frac{K}{\delta}\sqrt{d K T^{1+2\epsilon} \ln \frac{K}{\delta} \frac{1}{\epsilon}})$ that holds with probability $1-\delta$ under the mean-variance criterion with risk tolerance $\rho$, for any $0<\epsilon<\frac{1}{2}$, $0<\delta<1$. The empirical performance of our proposed algorithms is demonstrated via a portfolio selection problem.

Design of optical voltage sensor based on electric field regulation and rotating isomerism electrode

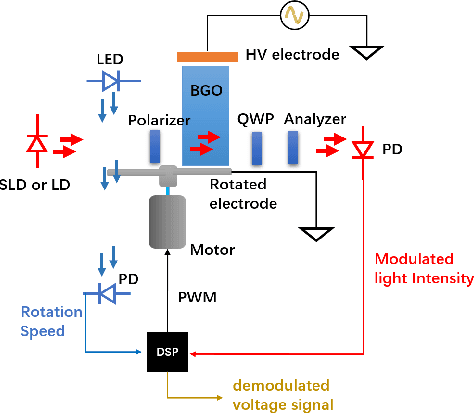
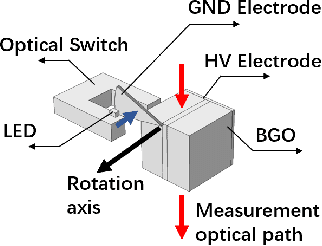
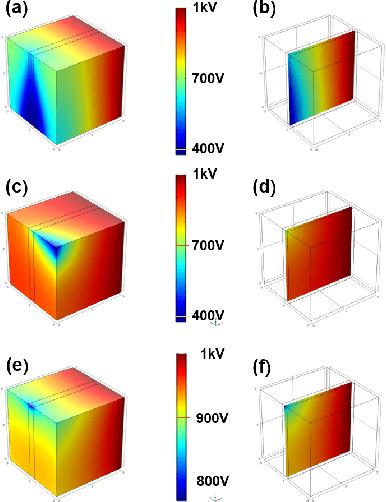
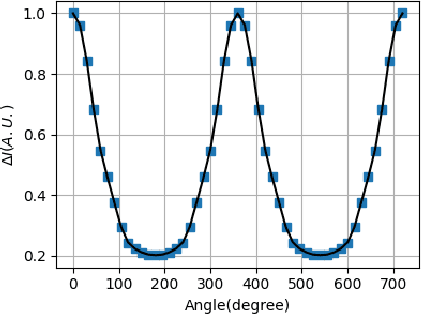
Temperature drift, stress birefringence and low frequency vibration lead to the randomness and fluctuation of the output of optical voltage sensor(OVS). In order to solve the problem, this study adopts the lock-in amplifier technology with the aid of a high-speed rotating electrode to realize electric field modulation. This technology could shift the measured signal frequency band from near 50 Hz moved to several kilometer Hz, so as to make the output signal avoid the interference from low-frequency temperature drift, stress birefringence and vibration, leading to higher stability and reliability. The electro-optic coupling wave theory and static electric field finite element method are utilized to investigate the shape of modulation wave. The simulation results proves that lock-in technology is able to prevent the measured voltage signal from the large step signal interference and restore the perfect original signal. While the sample rate is decreased to the value of the modulation frequency.