Risk-averse Contextual Multi-armed Bandit Problem with Linear Payoffs
Paper and Code
Jun 24, 2022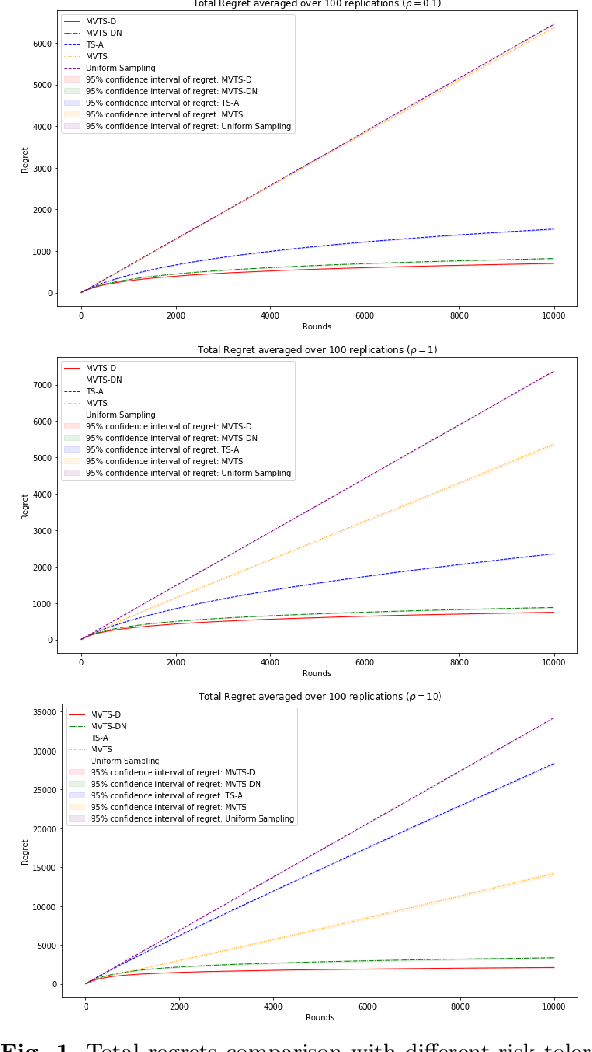
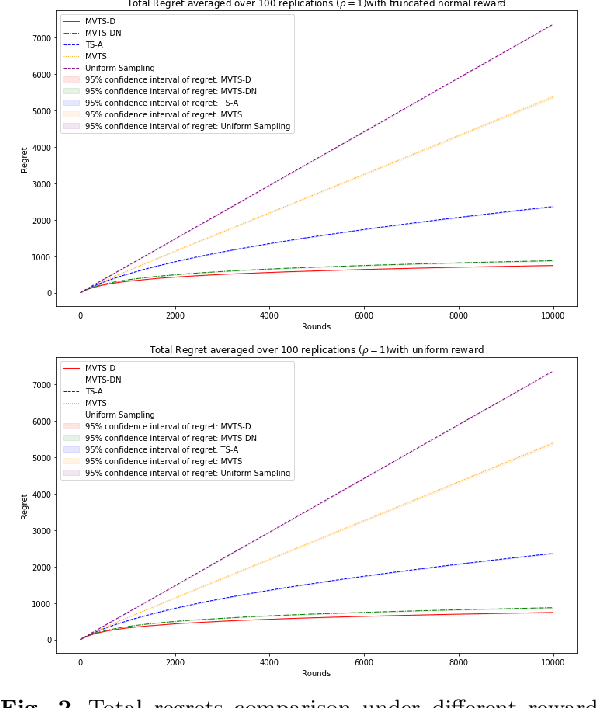
In this paper we consider the contextual multi-armed bandit problem for linear payoffs under a risk-averse criterion. At each round, contexts are revealed for each arm, and the decision maker chooses one arm to pull and receives the corresponding reward. In particular, we consider mean-variance as the risk criterion, and the best arm is the one with the largest mean-variance reward. We apply the Thompson Sampling algorithm for the disjoint model, and provide a comprehensive regret analysis for a variant of the proposed algorithm. For $T$ rounds, $K$ actions, and $d$-dimensional feature vectors, we prove a regret bound of $O((1+\rho+\frac{1}{\rho}) d\ln T \ln \frac{K}{\delta}\sqrt{d K T^{1+2\epsilon} \ln \frac{K}{\delta} \frac{1}{\epsilon}})$ that holds with probability $1-\delta$ under the mean-variance criterion with risk tolerance $\rho$, for any $0<\epsilon<\frac{1}{2}$, $0<\delta<1$. The empirical performance of our proposed algorithms is demonstrated via a portfolio selection problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge