Geometric Interaction Augmented Graph Collaborative Filtering

Graph-based collaborative filtering is capable of capturing the essential and abundant collaborative signals from the high-order interactions, and thus received increasingly research interests. Conventionally, the embeddings of users and items are defined in the Euclidean spaces, along with the propagation on the interaction graphs. Meanwhile, recent works point out that the high-order interactions naturally form up the tree-likeness structures, which the hyperbolic models thrive on. However, the interaction graphs inherently exhibit the hybrid and nested geometric characteristics, while the existing single geometry-based models are inadequate to fully capture such sophisticated topological patterns. In this paper, we propose to model the user-item interactions in a hybrid geometric space, in which the merits of Euclidean and hyperbolic spaces are simultaneously enjoyed to learn expressive representations. Experimental results on public datasets validate the effectiveness of our proposal.

Lorentzian Graph Convolutional Networks

Graph convolutional networks (GCNs) have received considerable research attention recently. Most GCNs learn the node representations in Euclidean geometry, but that could have a high distortion in the case of embedding graphs with scale-free or hierarchical structure. Recently, some GCNs are proposed to deal with this problem in non-Euclidean geometry, e.g., hyperbolic geometry. Although hyperbolic GCNs achieve promising performance, existing hyperbolic graph operations actually cannot rigorously follow the hyperbolic geometry, which may limit the ability of hyperbolic geometry and thus hurt the performance of hyperbolic GCNs. In this paper, we propose a novel hyperbolic GCN named Lorentzian graph convolutional network (LGCN), which rigorously guarantees the learned node features follow the hyperbolic geometry. Specifically, we rebuild the graph operations of hyperbolic GCNs with Lorentzian version, e.g., the feature transformation and non-linear activation. Also, an elegant neighborhood aggregation method is designed based on the centroid of Lorentzian distance. Moreover, we prove some proposed graph operations are equivalent in different types of hyperbolic geometry, which fundamentally indicates their correctness. Experiments on six datasets show that LGCN performs better than the state-of-the-art methods. LGCN has lower distortion to learn the representation of tree-likeness graphs compared with existing hyperbolic GCNs. We also find that the performance of some hyperbolic GCNs can be improved by simply replacing the graph operations with those we defined in this paper.

Robust Autonomous Landing of UAV in Non-Cooperative Environments based on Dynamic Time Camera-LiDAR Fusion

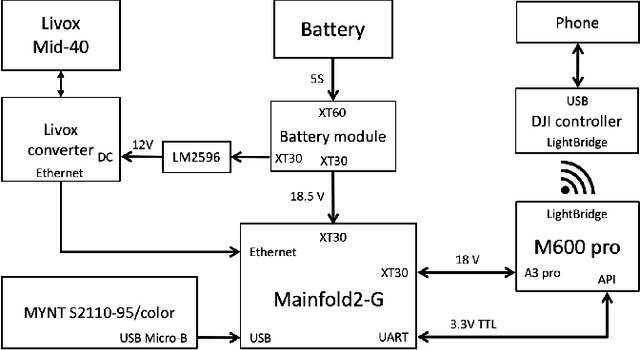
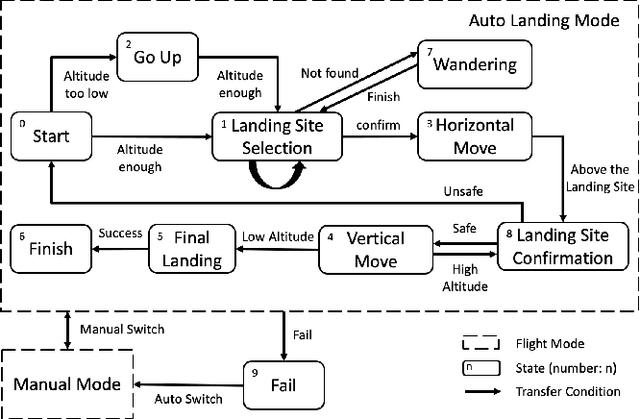
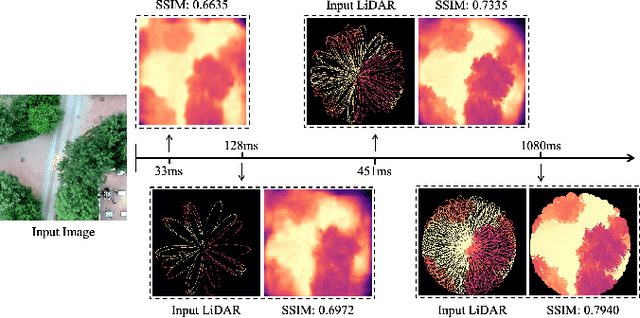
Selecting safe landing sites in non-cooperative environments is a key step towards the full autonomy of UAVs. However, the existing methods have the common problems of poor generalization ability and robustness. Their performance in unknown environments is significantly degraded and the error cannot be self-detected and corrected. In this paper, we construct a UAV system equipped with low-cost LiDAR and binocular cameras to realize autonomous landing in non-cooperative environments by detecting the flat and safe ground area. Taking advantage of the non-repetitive scanning and high FOV coverage characteristics of LiDAR, we come up with a dynamic time depth completion algorithm. In conjunction with the proposed self-evaluation method of the depth map, our model can dynamically select the LiDAR accumulation time at the inference phase to ensure an accurate prediction result. Based on the depth map, the high-level terrain information such as slope, roughness, and the size of the safe area are derived. We have conducted extensive autonomous landing experiments in a variety of familiar or completely unknown environments, verifying that our model can adaptively balance the accuracy and speed, and the UAV can robustly select a safe landing site.

Hyperbolic Graph Attention Network

Graph neural network (GNN) has shown superior performance in dealing with graphs, which has attracted considerable research attention recently. However, most of the existing GNN models are primarily designed for graphs in Euclidean spaces. Recent research has proven that the graph data exhibits non-Euclidean latent anatomy. Unfortunately, there was rarely study of GNN in non-Euclidean settings so far. To bridge this gap, in this paper, we study the GNN with attention mechanism in hyperbolic spaces at the first attempt. The research of hyperbolic GNN has some unique challenges: since the hyperbolic spaces are not vector spaces, the vector operations (e.g., vector addition, subtraction, and scalar multiplication) cannot be carried. To tackle this problem, we employ the gyrovector spaces, which provide an elegant algebraic formalism for hyperbolic geometry, to transform the features in a graph; and then we propose the hyperbolic proximity based attention mechanism to aggregate the features. Moreover, as mathematical operations in hyperbolic spaces could be more complicated than those in Euclidean spaces, we further devise a novel acceleration strategy using logarithmic and exponential mappings to improve the efficiency of our proposed model. The comprehensive experimental results on four real-world datasets demonstrate the performance of our proposed hyperbolic graph attention network model, by comparisons with other state-of-the-art baseline methods.