Preprocessing-based Kinodynamic Motion Planning Framework for Intercepting Projectiles using a Robot Manipulator

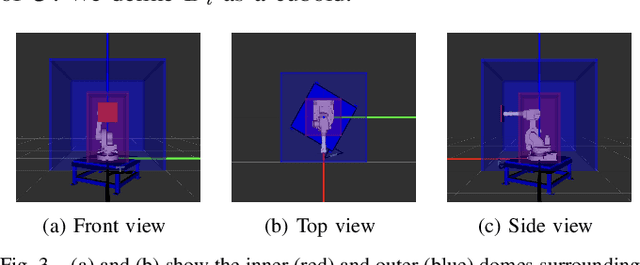
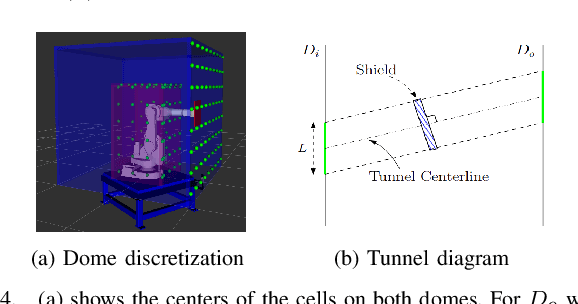
We are interested in studying sports with robots and starting with the problem of intercepting a projectile moving toward a robot manipulator equipped with a shield. To successfully perform this task, the robot needs to (i) detect the incoming projectile, (ii) predict the projectile's future motion, (iii) plan a minimum-time rapid trajectory that can evade obstacles and intercept the projectile, and (iv) execute the planned trajectory. These four steps must be performed under the manipulator's dynamic limits and extreme time constraints (<350ms in our setting) to successfully intercept the projectile. In addition, we want these trajectories to be smooth to reduce the robot's joint torques and the impulse on the platform on which it is mounted. To this end, we propose a kinodynamic motion planning framework that preprocesses smooth trajectories offline to allow real-time collision-free executions online. We present an end-to-end pipeline along with our planning framework, including perception, prediction, and execution modules. We evaluate our framework experimentally in simulation and show that it has a higher blocking success rate than the baselines. Further, we deploy our pipeline on a robotic system comprising an industrial arm (ABB IRB-1600) and an onboard stereo camera (ZED 2i), which achieves a 78% success rate in projectile interceptions.

Planning and Execution using Inaccurate Models with Provable Guarantees

Models used in modern planning problems to simulate outcomes of real world action executions are becoming increasingly complex, ranging from simulators that do physics-based reasoning to precomputed analytical motion primitives. However, robots operating in the real world often face situations not modeled by these models before execution. This imperfect modeling can lead to highly suboptimal or even incomplete behavior during execution. In this paper, we propose an approach for interleaving planning and execution that adapts online using real world execution and accounts for any discrepancies in dynamics during planning, without requiring updates to the dynamics of the model. This is achieved by biasing the planner away from transitions whose dynamics are discovered to be inaccurately modeled, thereby leading to robot behavior that tries to complete the task despite having an inaccurate model. We provide provable guarantees on the completeness and efficiency of the proposed planning and execution framework under specific assumptions on the model, for both small and large state spaces. Our approach is shown to be efficient empirically in simulated robotic tasks including 4D planar pushing, and in real robotic experiments using PR2 involving a 3D pick-and-place task where the mass of the object is incorrectly modeled, and a 7D arm planning task where one of the joints is not operational leading to discrepancy in dynamics. Video can be found at https://youtu.be/eQmAeWIhjO8

Trajectory Optimization for Curvature Bounded Non-Holonomic Vehicles: Application to Autonomous Driving

In this paper, we propose a trajectory optimization for computing smooth collision free trajectories for nonholonomic curvature bounded vehicles among static and dynamic obstacles. One of the key novelties of our formulation is a hierarchal optimization routine which alternately operates in the space of angular accelerations and linear velocities. That is, the optimization has a two layer structure wherein angular accelerations are optimized keeping the linear velocities fixed and vice versa. If the vehicle/obstacles are modeled as circles than the velocity optimization layer can be shown to have the computationally efficient difference of convex structure commonly observed for linear systems. This leads to a less conservative approximation as compared to that obtained by approximating each polygon individually through its circumscribing circle. On the other hand, it leads to optimization problem with less number of constraints as compared to that obtained when approximating polygons as multiple overlapping circles. We use the proposed trajectory optimization as the basis for constructing a Model Predictive Control framework for navigating an autonomous car in complex scenarios like overtaking, lane changing and merging. Moreover, we also highlight the advantages provided by the alternating optimization routine. Specifically, we show it produces trajectories which have comparable arc lengths and smoothness as compared to those produced with joint simultaneous optimization in the space of angular accelerations and linear velocities. However, importantly, the alternating optimization provides some gain in computational time.

Model Predictive Control for Autonomous Driving Based on Time Scaled Collision Cone

In this paper, we present a Model Predictive Control (MPC) framework based on path velocity decomposition paradigm for autonomous driving. The optimization underlying the MPC has a two layer structure wherein first, an appropriate path is computed for the vehicle followed by the computation of optimal forward velocity along it. The very nature of the proposed path velocity decomposition allows for seamless compatibility between the two layers of the optimization. A key feature of the proposed work is that it offloads most of the responsibility of collision avoidance to velocity optimization layer for which computationally efficient formulations can be derived. In particular, we extend our previously developed concept of time scaled collision cone (TSCC) constraints and formulate the forward velocity optimization layer as a convex quadratic programming problem. We perform validation on autonomous driving scenarios wherein proposed MPC repeatedly solves both the optimization layers in receding horizon manner to compute lane change, overtaking and merging maneuvers among multiple dynamic obstacles.