Fast Adaptation of Manipulator Trajectories to Task Perturbation By Differentiating through the Optimal Solution

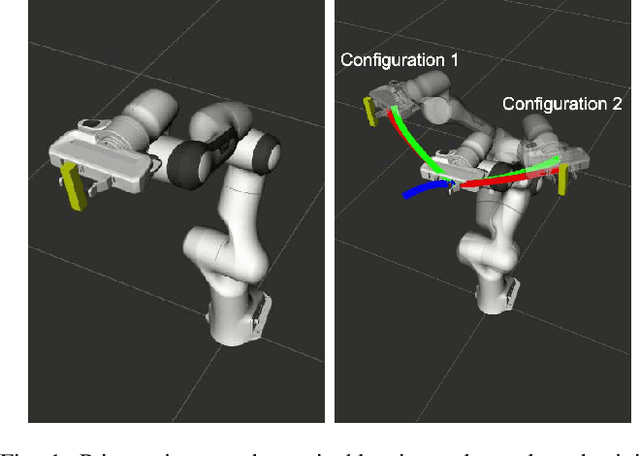
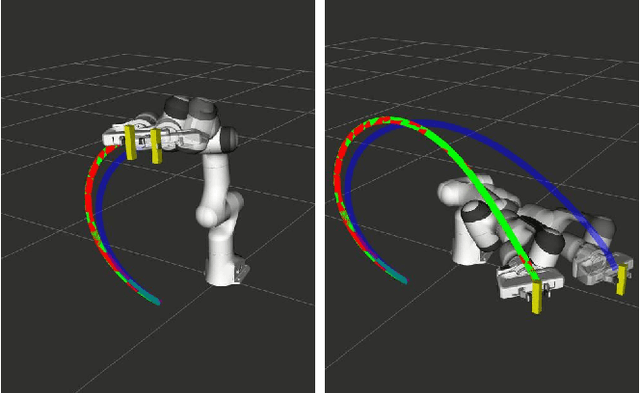
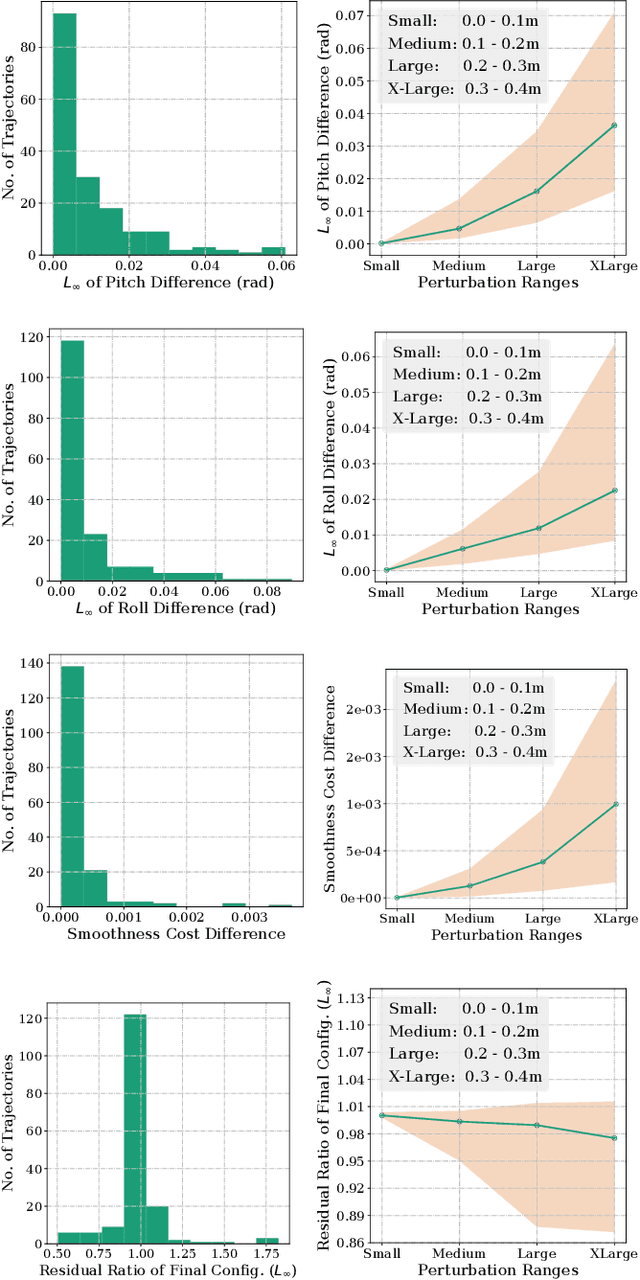
Joint space trajectory optimization under end-effector task constraints leads to a challenging non-convex problem. Thus, a real-time adaptation of prior computed trajectories to perturbation in task constraints often becomes intractable. Existing works use the so-called warm-starting of trajectory optimization to improve computational performance. We present a fundamentally different approach that relies on deriving analytical gradients of the optimal solution with respect to the task constraint parameters. This gradient map characterizes the direction in which the prior computed joint trajectories need to be deformed to comply with the new task constraints. Subsequently, we develop an iterative line-search algorithm for computing the scale of deformation. Our algorithm provides near real-time adaptation of joint trajectories for a diverse class of task perturbations such as (i) changes in initial and final joint configurations of end-effector orientation-constrained trajectories and (ii) changes in end-effector goal or way-points under end-effector orientation constraints. We relate each of these examples to real-world applications ranging from learning from demonstration to obstacle avoidance. We also show that our algorithm produces trajectories with quality similar to what one would obtain by solving the trajectory optimization from scratch with warm-start initialization. But most importantly, our algorithm achieves a worst-case speed-up of 160x over the latter approach.

Model Predictive Control for Autonomous Driving considering Actuator Dynamics

In this paper, we propose a new model predictive control (MPC) formulation for autonomous driving. The novelty of our MPC stems from the following results. Firstly, we adopt an alternating minimization approach wherein linear velocities and angular accelerations are alternately optimized. We show that in contrast to the joint optimization, the alternating minimization exploits the structure of the problem better, which in turn translates to reduction in computation time. Secondly, our MPC explicitly incorporates the time dependent non-linear actuator dynamics that captures the transient response of the vehicle for a given commanded velocity. This added complexity improves the predictive component of MPC resulting in improved margin of inter-vehicle distance during maneuvers like overtaking, lane-change, etc. Although, past works have also incorporated actuator dynamics within MPC, there has been very few attempts towards coupling actuator dynamics to collision avoidance constraints through the non-holonomic motion model of the vehicle and analyzing the resulting behavior. We use a high fidelity simulator to benchmark our actuator dynamics augmented MPC with other related approaches in terms of metrics like inter-vehicle distance, trajectory smoothness, and velocity overshoot.

Trajectory Optimization for Curvature Bounded Non-Holonomic Vehicles: Application to Autonomous Driving

In this paper, we propose a trajectory optimization for computing smooth collision free trajectories for nonholonomic curvature bounded vehicles among static and dynamic obstacles. One of the key novelties of our formulation is a hierarchal optimization routine which alternately operates in the space of angular accelerations and linear velocities. That is, the optimization has a two layer structure wherein angular accelerations are optimized keeping the linear velocities fixed and vice versa. If the vehicle/obstacles are modeled as circles than the velocity optimization layer can be shown to have the computationally efficient difference of convex structure commonly observed for linear systems. This leads to a less conservative approximation as compared to that obtained by approximating each polygon individually through its circumscribing circle. On the other hand, it leads to optimization problem with less number of constraints as compared to that obtained when approximating polygons as multiple overlapping circles. We use the proposed trajectory optimization as the basis for constructing a Model Predictive Control framework for navigating an autonomous car in complex scenarios like overtaking, lane changing and merging. Moreover, we also highlight the advantages provided by the alternating optimization routine. Specifically, we show it produces trajectories which have comparable arc lengths and smoothness as compared to those produced with joint simultaneous optimization in the space of angular accelerations and linear velocities. However, importantly, the alternating optimization provides some gain in computational time.

Model Predictive Control for Autonomous Driving Based on Time Scaled Collision Cone

In this paper, we present a Model Predictive Control (MPC) framework based on path velocity decomposition paradigm for autonomous driving. The optimization underlying the MPC has a two layer structure wherein first, an appropriate path is computed for the vehicle followed by the computation of optimal forward velocity along it. The very nature of the proposed path velocity decomposition allows for seamless compatibility between the two layers of the optimization. A key feature of the proposed work is that it offloads most of the responsibility of collision avoidance to velocity optimization layer for which computationally efficient formulations can be derived. In particular, we extend our previously developed concept of time scaled collision cone (TSCC) constraints and formulate the forward velocity optimization layer as a convex quadratic programming problem. We perform validation on autonomous driving scenarios wherein proposed MPC repeatedly solves both the optimization layers in receding horizon manner to compute lane change, overtaking and merging maneuvers among multiple dynamic obstacles.