Reactive Navigation under Non-Parametric Uncertainty through Hilbert Space Embedding of Probabilistic Velocity Obstacles

The probabilistic velocity obstacle (PVO) extends the concept of velocity obstacle (VO) to work in uncertain dynamic environments. In this paper, we show how a robust model predictive control (MPC) with PVO constraints under non-parametric uncertainty can be made computationally tractable. At the core of our formulation is a novel yet simple interpretation of our robust MPC as a problem of matching the distribution of PVO with a certain desired distribution. To this end, we propose two methods. Our first baseline method is based on approximating the distribution of PVO with a Gaussian Mixture Model (GMM) and subsequently performing distribution matching using Kullback Leibler (KL) divergence metric. Our second formulation is based on the possibility of representing arbitrary distributions as functions in Reproducing Kernel Hilbert Space (RKHS). We use this foundation to interpret our robust MPC as a problem of minimizing the distance between the desired distribution and the distribution of the PVO in the RKHS. Both the RKHS and GMM based formulation can work with any uncertainty distribution and thus allowing us to relax the prevalent Gaussian assumption in the existing works. We validate our formulation by taking an example of 2D navigation of quadrotors with a realistic noise model for perception and ego-motion uncertainty. In particular, we present a systematic comparison between the GMM and the RKHS approach and show that while both approaches can produce safe trajectories, the former is highly conservative and leads to poor tracking and control costs. Furthermore, RKHS based approach gives better computational times that are up to one order of magnitude lesser than the computation time of the GMM based approach.

Solving Chance Constrained Optimization under Non-Parametric Uncertainty Through Hilbert Space Embedding

In this paper, we present an efficient algorithm for solving a class of chance constrained optimization under non-parametric uncertainty. Our algorithm is built on the possibility of representing arbitrary distributions as functions in Reproducing Kernel Hilbert Space (RKHS). We use this foundation to formulate chance constrained optimization as one of minimizing the distance between a desired distribution and the distribution of the constraint functions in the RKHS. We provide a systematic way of constructing the desired distribution based on a notion of scenario approximation. Furthermore, we use the kernel trick to show that the computational complexity of our reformulated optimization problem is comparable to solving a deterministic variant of the chance-constrained optimization. We validate our formulation on two important robotic/control applications: (i) reactive collision avoidance of mobile robots in uncertain dynamic environments and (ii) inverse dynamics based path tracking of manipulators under perception uncertainty. In both these applications, the underlying chance constraints are defined over highly non-linear and non-convex functions of the uncertain parameters and possibly also decision variables. We also benchmark our formulation with the existing approaches in terms of sample complexity and the achieved optimal cost highlighting significant improvements in both these metrics.

Model Predictive Control for Autonomous Driving considering Actuator Dynamics

In this paper, we propose a new model predictive control (MPC) formulation for autonomous driving. The novelty of our MPC stems from the following results. Firstly, we adopt an alternating minimization approach wherein linear velocities and angular accelerations are alternately optimized. We show that in contrast to the joint optimization, the alternating minimization exploits the structure of the problem better, which in turn translates to reduction in computation time. Secondly, our MPC explicitly incorporates the time dependent non-linear actuator dynamics that captures the transient response of the vehicle for a given commanded velocity. This added complexity improves the predictive component of MPC resulting in improved margin of inter-vehicle distance during maneuvers like overtaking, lane-change, etc. Although, past works have also incorporated actuator dynamics within MPC, there has been very few attempts towards coupling actuator dynamics to collision avoidance constraints through the non-holonomic motion model of the vehicle and analyzing the resulting behavior. We use a high fidelity simulator to benchmark our actuator dynamics augmented MPC with other related approaches in terms of metrics like inter-vehicle distance, trajectory smoothness, and velocity overshoot.

Chance constraint based multi agent navigation under uncertainty

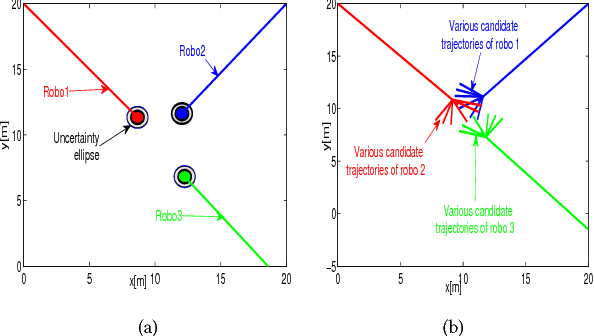
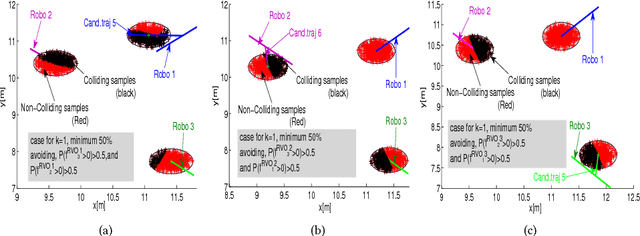
We present Probabilistic Reciprocal Velocity Obstacle or PRVO as a general algorithm for navigating multiple robots under perception and motion uncertainty. PRVO is defined as the space of velocities that ensures dynamic collision avoidance between a pair of robots with a specified probability. Our approach is based on defining chance constraints over the inequalities defined by the deterministic Reciprocal Velocity Obstacle (RVO). The computational complexity of the proposed probabilistic RVO is comparable to the deterministic counterpart. This is achieved by a series of reformulations where we first substitute the computationally intractable chance constraints with a family of surrogate constraints and then adopt a time scaling based solution methodology to efficiently characterize their solution space. Further, we also show that the solution space of each member of the family of surrogate constraints can be mapped in closed form to the probability with which the original chance constraints are satisfied and thus consequently to probability of collision avoidance. We validate our formulations through numerical simulations where we highlight the importance of incorporating the effect of motion uncertainty and the advantages of PRVO over existing formulations which handles the effect of uncertainty by using conservative bounding volumes.