Look At Me, No Replay! SurpriseNet: Anomaly Detection Inspired Class Incremental Learning

Continual learning aims to create artificial neural networks capable of accumulating knowledge and skills through incremental training on a sequence of tasks. The main challenge of continual learning is catastrophic interference, wherein new knowledge overrides or interferes with past knowledge, leading to forgetting. An associated issue is the problem of learning "cross-task knowledge," where models fail to acquire and retain knowledge that helps differentiate classes across task boundaries. A common solution to both problems is "replay," where a limited buffer of past instances is utilized to learn cross-task knowledge and mitigate catastrophic interference. However, a notable drawback of these methods is their tendency to overfit the limited replay buffer. In contrast, our proposed solution, SurpriseNet, addresses catastrophic interference by employing a parameter isolation method and learning cross-task knowledge using an auto-encoder inspired by anomaly detection. SurpriseNet is applicable to both structured and unstructured data, as it does not rely on image-specific inductive biases. We have conducted empirical experiments demonstrating the strengths of SurpriseNet on various traditional vision continual-learning benchmarks, as well as on structured data datasets. Source code made available at https://doi.org/10.5281/zenodo.8247906 and https://github.com/tachyonicClock/SurpriseNet-CIKM-23

A simple but strong baseline for online continual learning: Repeated Augmented Rehearsal

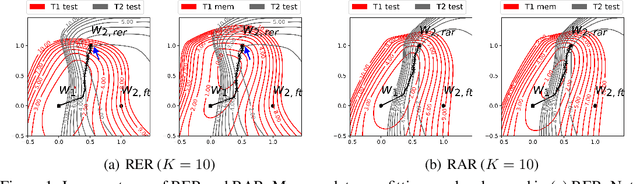
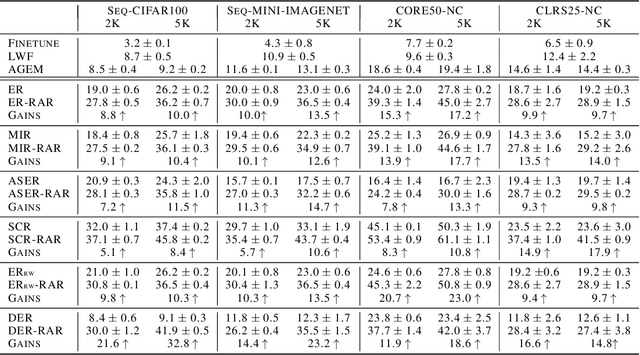
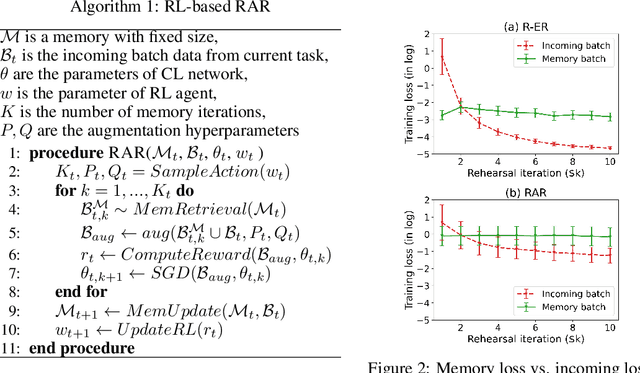
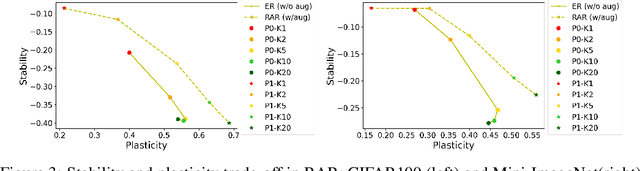
Online continual learning (OCL) aims to train neural networks incrementally from a non-stationary data stream with a single pass through data. Rehearsal-based methods attempt to approximate the observed input distributions over time with a small memory and revisit them later to avoid forgetting. Despite its strong empirical performance, rehearsal methods still suffer from a poor approximation of the loss landscape of past data with memory samples. This paper revisits the rehearsal dynamics in online settings. We provide theoretical insights on the inherent memory overfitting risk from the viewpoint of biased and dynamic empirical risk minimization, and examine the merits and limits of repeated rehearsal. Inspired by our analysis, a simple and intuitive baseline, Repeated Augmented Rehearsal (RAR), is designed to address the underfitting-overfitting dilemma of online rehearsal. Surprisingly, across four rather different OCL benchmarks, this simple baseline outperforms vanilla rehearsal by 9%-17% and also significantly improves state-of-the-art rehearsal-based methods MIR, ASER, and SCR. We also demonstrate that RAR successfully achieves an accurate approximation of the loss landscape of past data and high-loss ridge aversion in its learning trajectory. Extensive ablation studies are conducted to study the interplay between repeated and augmented rehearsal and reinforcement learning (RL) is applied to dynamically adjust the hyperparameters of RAR to balance the stability-plasticity trade-off online.

A Graph-Based Semi-Supervised k Nearest-Neighbor Method for Nonlinear Manifold Distributed Data Classification

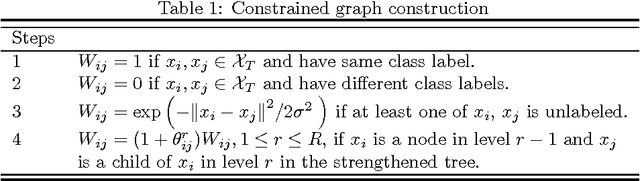
$k$ Nearest Neighbors ($k$NN) is one of the most widely used supervised learning algorithms to classify Gaussian distributed data, but it does not achieve good results when it is applied to nonlinear manifold distributed data, especially when a very limited amount of labeled samples are available. In this paper, we propose a new graph-based $k$NN algorithm which can effectively handle both Gaussian distributed data and nonlinear manifold distributed data. To achieve this goal, we first propose a constrained Tired Random Walk (TRW) by constructing an $R$-level nearest-neighbor strengthened tree over the graph, and then compute a TRW matrix for similarity measurement purposes. After this, the nearest neighbors are identified according to the TRW matrix and the class label of a query point is determined by the sum of all the TRW weights of its nearest neighbors. To deal with online situations, we also propose a new algorithm to handle sequential samples based a local neighborhood reconstruction. Comparison experiments are conducted on both synthetic data sets and real-world data sets to demonstrate the validity of the proposed new $k$NN algorithm and its improvements to other version of $k$NN algorithms. Given the widespread appearance of manifold structures in real-world problems and the popularity of the traditional $k$NN algorithm, the proposed manifold version $k$NN shows promising potential for classifying manifold-distributed data.