A Graph-Based Semi-Supervised k Nearest-Neighbor Method for Nonlinear Manifold Distributed Data Classification
Paper and Code
Jun 03, 2016
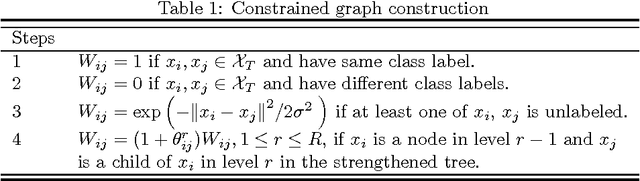


$k$ Nearest Neighbors ($k$NN) is one of the most widely used supervised learning algorithms to classify Gaussian distributed data, but it does not achieve good results when it is applied to nonlinear manifold distributed data, especially when a very limited amount of labeled samples are available. In this paper, we propose a new graph-based $k$NN algorithm which can effectively handle both Gaussian distributed data and nonlinear manifold distributed data. To achieve this goal, we first propose a constrained Tired Random Walk (TRW) by constructing an $R$-level nearest-neighbor strengthened tree over the graph, and then compute a TRW matrix for similarity measurement purposes. After this, the nearest neighbors are identified according to the TRW matrix and the class label of a query point is determined by the sum of all the TRW weights of its nearest neighbors. To deal with online situations, we also propose a new algorithm to handle sequential samples based a local neighborhood reconstruction. Comparison experiments are conducted on both synthetic data sets and real-world data sets to demonstrate the validity of the proposed new $k$NN algorithm and its improvements to other version of $k$NN algorithms. Given the widespread appearance of manifold structures in real-world problems and the popularity of the traditional $k$NN algorithm, the proposed manifold version $k$NN shows promising potential for classifying manifold-distributed data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge