Nikola Kasabov
A Novel Explainable Out-of-Distribution Detection Approach for Spiking Neural Networks
Sep 30, 2022


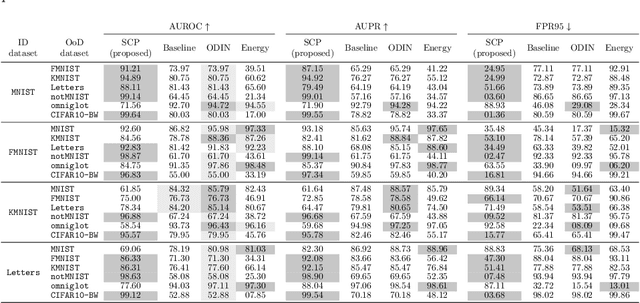
Abstract:Research around Spiking Neural Networks has ignited during the last years due to their advantages when compared to traditional neural networks, including their efficient processing and inherent ability to model complex temporal dynamics. Despite these differences, Spiking Neural Networks face similar issues than other neural computation counterparts when deployed in real-world settings. This work addresses one of the practical circumstances that can hinder the trustworthiness of this family of models: the possibility of querying a trained model with samples far from the distribution of its training data (also referred to as Out-of-Distribution or OoD data). Specifically, this work presents a novel OoD detector that can identify whether test examples input to a Spiking Neural Network belong to the distribution of the data over which it was trained. For this purpose, we characterize the internal activations of the hidden layers of the network in the form of spike count patterns, which lay a basis for determining when the activations induced by a test instance is atypical. Furthermore, a local explanation method is devised to produce attribution maps revealing which parts of the input instance push most towards the detection of an example as an OoD sample. Experimental results are performed over several image classification datasets to compare the proposed detector to other OoD detection schemes from the literature. As the obtained results clearly show, the proposed detector performs competitively against such alternative schemes, and produces relevance attribution maps that conform to expectations for synthetically created OoD instances.
Spiking Neural Networks and Online Learning: An Overview and Perspectives
Jul 23, 2019



Abstract:Applications that generate huge amounts of data in the form of fast streams are becoming increasingly prevalent, being therefore necessary to learn in an online manner. These conditions usually impose memory and processing time restrictions, and they often turn into evolving environments where a change may affect the input data distribution. Such a change causes that predictive models trained over these stream data become obsolete and do not adapt suitably to new distributions. Specially in these non-stationary scenarios, there is a pressing need for new algorithms that adapt to these changes as fast as possible, while maintaining good performance scores. Unfortunately, most off-the-shelf classification models need to be retrained if they are used in changing environments, and fail to scale properly. Spiking Neural Networks have revealed themselves as one of the most successful approaches to model the behavior and learning potential of the brain, and exploit them to undertake practical online learning tasks. Besides, some specific flavors of Spiking Neural Networks can overcome the necessity of retraining after a drift occurs. This work intends to merge both fields by serving as a comprehensive overview, motivating further developments that embrace Spiking Neural Networks for online learning scenarios, and being a friendly entry point for non-experts.
A Graph-Based Semi-Supervised k Nearest-Neighbor Method for Nonlinear Manifold Distributed Data Classification
Jun 03, 2016
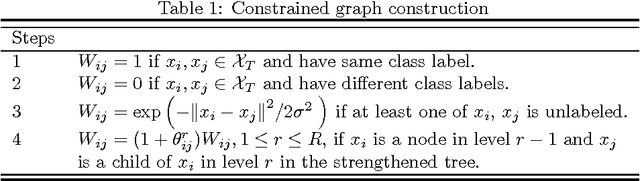


Abstract:$k$ Nearest Neighbors ($k$NN) is one of the most widely used supervised learning algorithms to classify Gaussian distributed data, but it does not achieve good results when it is applied to nonlinear manifold distributed data, especially when a very limited amount of labeled samples are available. In this paper, we propose a new graph-based $k$NN algorithm which can effectively handle both Gaussian distributed data and nonlinear manifold distributed data. To achieve this goal, we first propose a constrained Tired Random Walk (TRW) by constructing an $R$-level nearest-neighbor strengthened tree over the graph, and then compute a TRW matrix for similarity measurement purposes. After this, the nearest neighbors are identified according to the TRW matrix and the class label of a query point is determined by the sum of all the TRW weights of its nearest neighbors. To deal with online situations, we also propose a new algorithm to handle sequential samples based a local neighborhood reconstruction. Comparison experiments are conducted on both synthetic data sets and real-world data sets to demonstrate the validity of the proposed new $k$NN algorithm and its improvements to other version of $k$NN algorithms. Given the widespread appearance of manifold structures in real-world problems and the popularity of the traditional $k$NN algorithm, the proposed manifold version $k$NN shows promising potential for classifying manifold-distributed data.
Mapping Temporal Variables into the NeuCube for Improved Pattern Recognition, Predictive Modelling and Understanding of Stream Data
Mar 17, 2016



Abstract:This paper proposes a new method for an optimized mapping of temporal variables, describing a temporal stream data, into the recently proposed NeuCube spiking neural network architecture. This optimized mapping extends the use of the NeuCube, which was initially designed for spatiotemporal brain data, to work on arbitrary stream data and to achieve a better accuracy of temporal pattern recognition, a better and earlier event prediction and a better understanding of complex temporal stream data through visualization of the NeuCube connectivity. The effect of the new mapping is demonstrated on three bench mark problems. The first one is early prediction of patient sleep stage event from temporal physiological data. The second one is pattern recognition of dynamic temporal patterns of traffic in the Bay Area of California and the last one is the Challenge 2012 contest data set. In all cases the use of the proposed mapping leads to an improved accuracy of pattern recognition and event prediction and a better understanding of the data when compared to traditional machine learning techniques or spiking neural network reservoirs with arbitrary mapping of the variables.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge