Towards an Understanding of Context Utilization in Code Intelligence

Code intelligence is an emerging domain in software engineering, aiming to improve the effectiveness and efficiency of various code-related tasks. Recent research suggests that incorporating contextual information beyond the basic original task inputs (i.e., source code) can substantially enhance model performance. Such contextual signals may be obtained directly or indirectly from sources such as API documentation or intermediate representations like abstract syntax trees can significantly improve the effectiveness of code intelligence. Despite growing academic interest, there is a lack of systematic analysis of context in code intelligence. To address this gap, we conduct an extensive literature review of 146 relevant studies published between September 2007 and August 2024. Our investigation yields four main contributions. (1) A quantitative analysis of the research landscape, including publication trends, venues, and the explored domains; (2) A novel taxonomy of context types used in code intelligence; (3) A task-oriented analysis investigating context integration strategies across diverse code intelligence tasks; (4) A critical evaluation of evaluation methodologies for context-aware methods. Based on these findings, we identify fundamental challenges in context utilization in current code intelligence systems and propose a research roadmap that outlines key opportunities for future research.

RepoTransBench: A Real-World Benchmark for Repository-Level Code Translation

Repository-level code translation refers to translating an entire code repository from one programming language to another while preserving the functionality of the source repository. Many benchmarks have been proposed to evaluate the performance of such code translators. However, previous benchmarks mostly provide fine-grained samples, focusing at either code snippet, function, or file-level code translation. Such benchmarks do not accurately reflect real-world demands, where entire repositories often need to be translated, involving longer code length and more complex functionalities. To address this gap, we propose a new benchmark, named RepoTransBench, which is a real-world repository-level code translation benchmark with an automatically executable test suite. We conduct experiments on RepoTransBench to evaluate the translation performance of 11 advanced LLMs. We find that the Success@1 score (test success in one attempt) of the best-performing LLM is only 7.33%. To further explore the potential of LLMs for repository-level code translation, we provide LLMs with error-related feedback to perform iterative debugging and observe an average 7.09% improvement on Success@1. However, even with this improvement, the Success@1 score of the best-performing LLM is only 21%, which may not meet the need for reliable automatic repository-level code translation. Finally, we conduct a detailed error analysis and highlight current LLMs' deficiencies in repository-level code translation, which could provide a reference for further improvements.

Diffusion Models in Bioinformatics: A New Wave of Deep Learning Revolution in Action

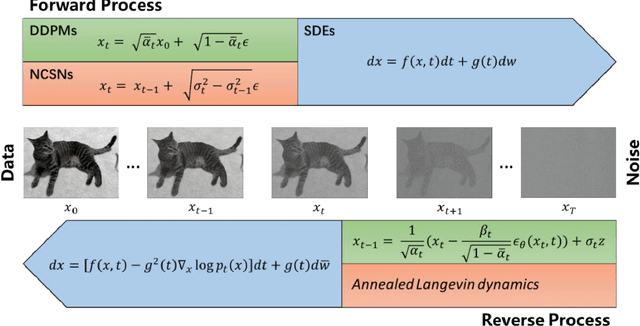
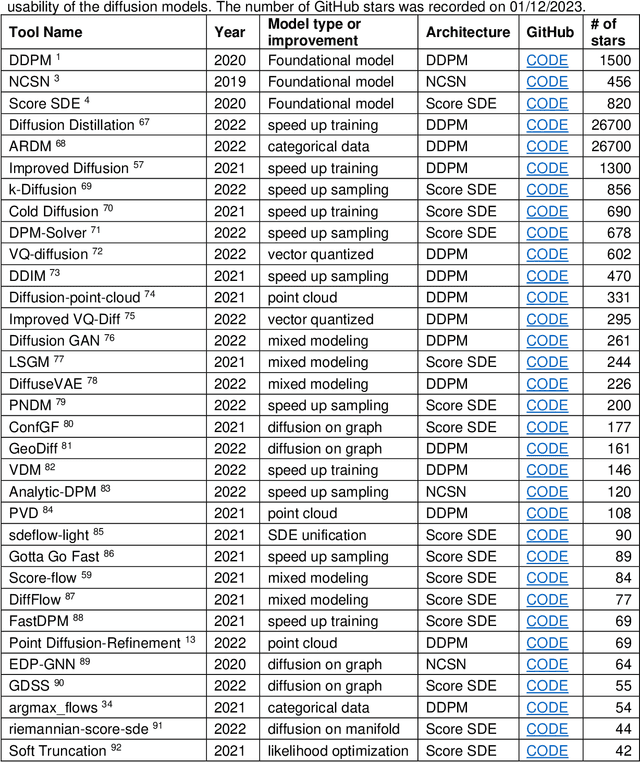
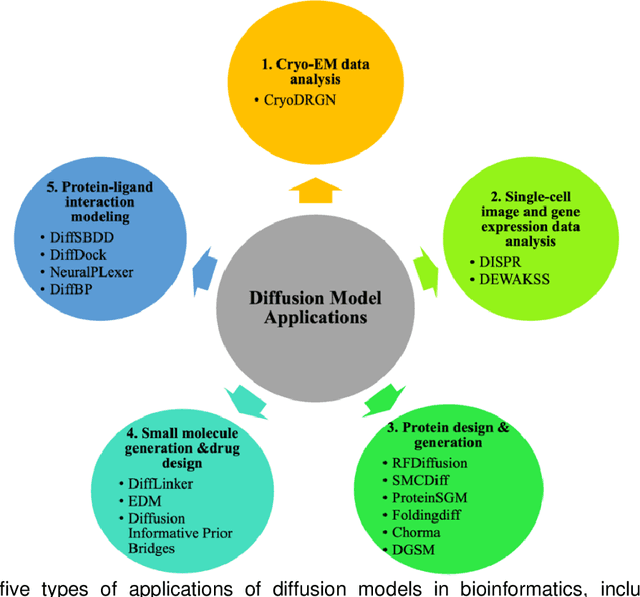
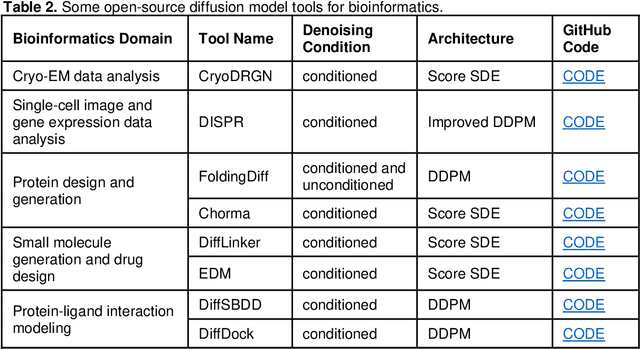
Denoising diffusion models have emerged as one of the most powerful generative models in recent years. They have achieved remarkable success in many fields, such as computer vision, natural language processing (NLP), and bioinformatics. Although there are a few excellent reviews on diffusion models and their applications in computer vision and NLP, there is a lack of an overview of their applications in bioinformatics. This review aims to provide a rather thorough overview of the applications of diffusion models in bioinformatics to aid their further development in bioinformatics and computational biology. We start with an introduction of the key concepts and theoretical foundations of three cornerstone diffusion modeling frameworks (denoising diffusion probabilistic models, noise-conditioned scoring networks, and stochastic differential equations), followed by a comprehensive description of diffusion models employed in the different domains of bioinformatics, including cryo-EM data enhancement, single-cell data analysis, protein design and generation, drug and small molecule design, and protein-ligand interaction. The review is concluded with a summary of the potential new development and applications of diffusion models in bioinformatics.

Heat Kernel Smoothing in Irregular Image Domains

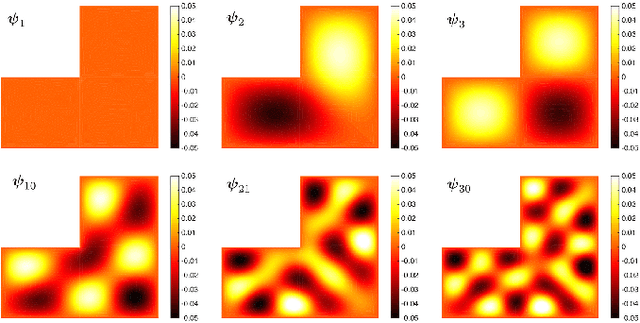
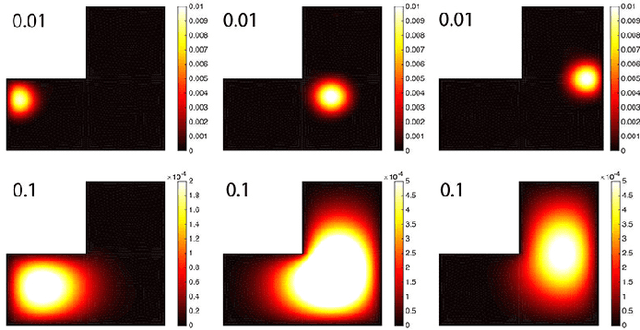
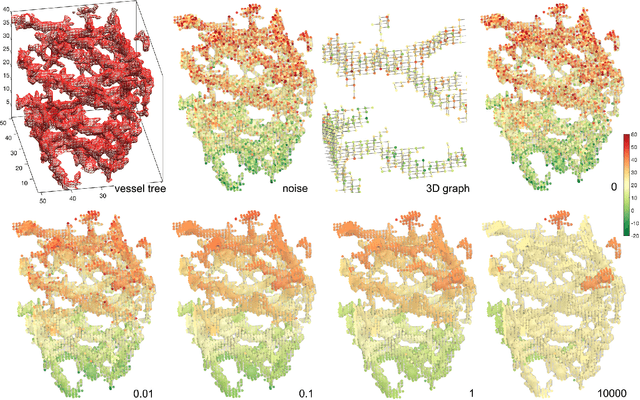
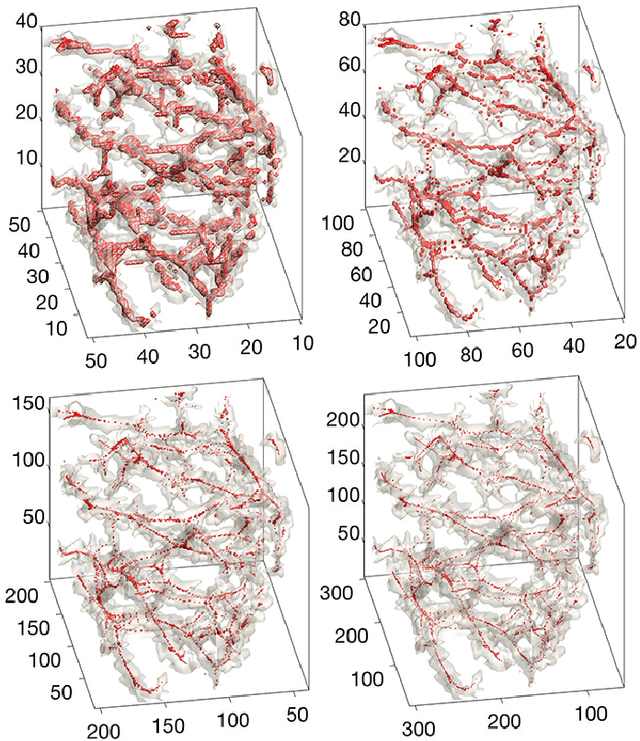
We present the discrete version of heat kernel smoothing on graph data structure. The method is used to smooth data in an irregularly shaped domains in 3D images. New statistical properties are derived. As an application, we show how to filter out data in the lung blood vessel trees obtained from computed tomography. The method can be further used in representing the complex vessel trees parametrically and extracting the skeleton representation of the trees.