Offline Policy Evaluation and Optimization under Confounding

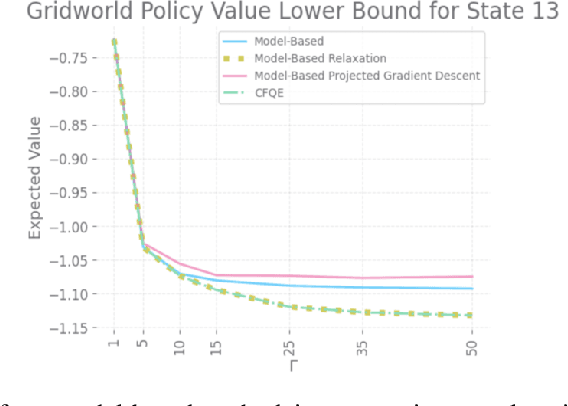
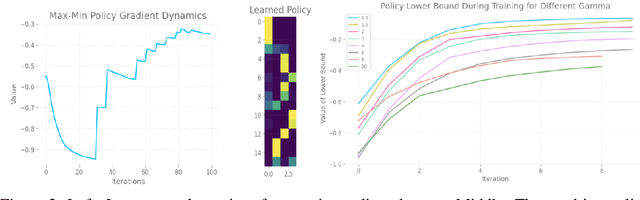
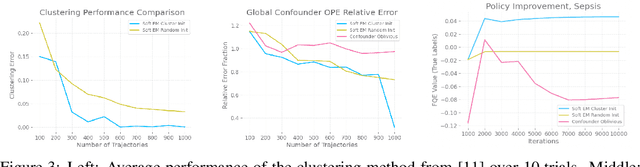
With a few exceptions, work in offline reinforcement learning (RL) has so far assumed that there is no confounding. In a classical regression setting, confounders introduce omitted variable bias and inhibit the identification of causal effects. In offline RL, they prevent the identification of a policy's value, and therefore make it impossible to perform policy improvement. Using conventional methods in offline RL in the presence of confounding can therefore not only lead to poor decisions and poor policies, but can also have disastrous effects in applications such as healthcare and education. We provide approaches for both off-policy evaluation (OPE) and local policy optimization in the settings of i.i.d. and global confounders. Theoretical and empirical results confirm the validity and viability of these methods.

Bandit Algorithms for Precision Medicine

The Oxford English Dictionary defines precision medicine as "medical care designed to optimize efficiency or therapeutic benefit for particular groups of patients, especially by using genetic or molecular profiling." It is not an entirely new idea: physicians from ancient times have recognized that medical treatment needs to consider individual variations in patient characteristics. However, the modern precision medicine movement has been enabled by a confluence of events: scientific advances in fields such as genetics and pharmacology, technological advances in mobile devices and wearable sensors, and methodological advances in computing and data sciences. This chapter is about bandit algorithms: an area of data science of special relevance to precision medicine. With their roots in the seminal work of Bellman, Robbins, Lai and others, bandit algorithms have come to occupy a central place in modern data science ( Lattimore and Szepesvari, 2020). Bandit algorithms can be used in any situation where treatment decisions need to be made to optimize some health outcome. Since precision medicine focuses on the use of patient characteristics to guide treatment, contextual bandit algorithms are especially useful since they are designed to take such information into account. The role of bandit algorithms in areas of precision medicine such as mobile health and digital phenotyping has been reviewed before (Tewari and Murphy, 2017; Rabbi et al., 2019). Since these reviews were published, bandit algorithms have continued to find uses in mobile health and several new topics have emerged in the research on bandit algorithms. This chapter is written for quantitative researchers in fields such as statistics, machine learning, and operations research who might be interested in knowing more about the algorithmic and mathematical details of bandit algorithms that have been used in mobile health.

Causal Bandits with Unknown Graph Structure

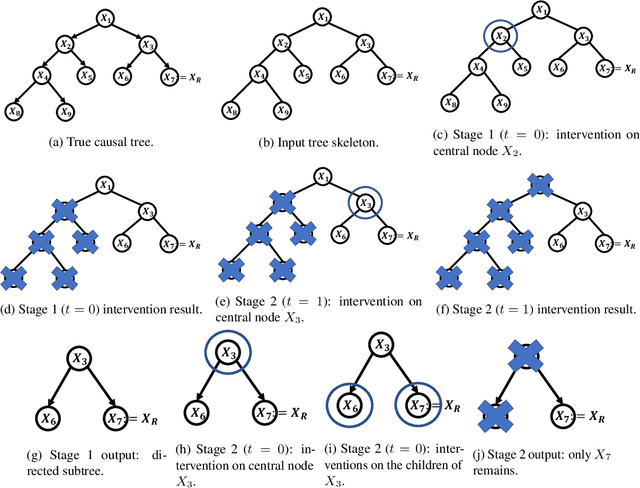
In causal bandit problems, the action set consists of interventions on variables of a causal graph. Several researchers have recently studied such bandit problems and pointed out their practical applications. However, all existing works rely on a restrictive and impractical assumption that the learner is given full knowledge of the causal graph structure upfront. In this paper, we develop novel causal bandit algorithms without knowing the causal graph. Our algorithms work well for causal trees, causal forests and a general class of causal graphs. The regret guarantees of our algorithms greatly improve upon those of standard multi-armed bandit (MAB) algorithms under mild conditions. Lastly, we prove our mild conditions are necessary: without them one cannot do better than standard MAB bandit algorithms.

Causal Markov Decision Processes: Learning Good Interventions Efficiently

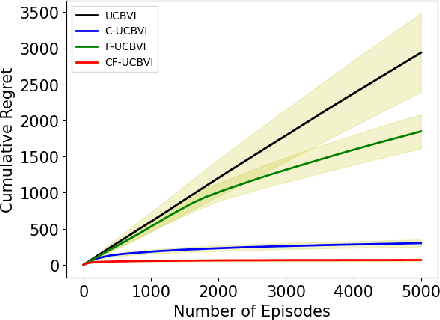
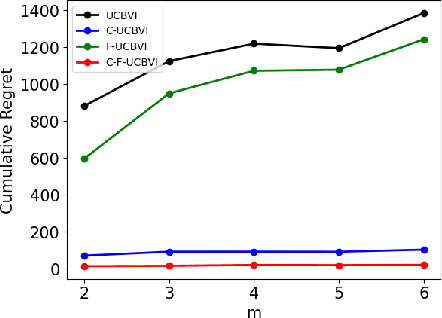
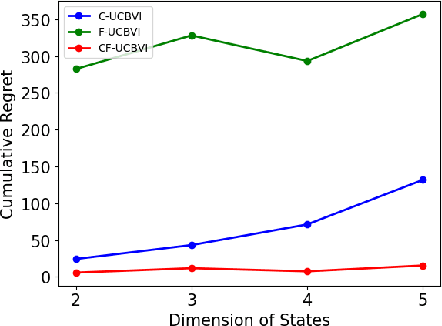
We introduce causal Markov Decision Processes (C-MDPs), a new formalism for sequential decision making which combines the standard MDP formulation with causal structures over state transition and reward functions. Many contemporary and emerging application areas such as digital healthcare and digital marketing can benefit from modeling with C-MDPs due to the causal mechanisms underlying the relationship between interventions and states/rewards. We propose the causal upper confidence bound value iteration (C-UCBVI) algorithm that exploits the causal structure in C-MDPs and improves the performance of standard reinforcement learning algorithms that do not take causal knowledge into account. We prove that C-UCBVI satisfies an $\tilde{O}(HS\sqrt{ZT})$ regret bound, where $T$ is the the total time steps, $H$ is the episodic horizon, and $S$ is the cardinality of the state space. Notably, our regret bound does not scale with the size of actions/interventions ($A$), but only scales with a causal graph dependent quantity $Z$ which can be exponentially smaller than $A$. By extending C-UCBVI to the factored MDP setting, we propose the causal factored UCBVI (CF-UCBVI) algorithm, which further reduces the regret exponentially in terms of $S$. Furthermore, we show that RL algorithms for linear MDP problems can also be incorporated in C-MDPs. We empirically show the benefit of our causal approaches in various settings to validate our algorithms and theoretical results.

Low-Rank Generalized Linear Bandit Problems

In a low-rank linear bandit problem, the reward of an action (represented by a matrix of size $d_1 \times d_2$) is the inner product between the action and an unknown low-rank matrix $\Theta^*$. We propose an algorithm based on a novel combination of online-to-confidence-set conversion~\citep{abbasi2012online} and the exponentially weighted average forecaster constructed by a covering of low-rank matrices. In $T$ rounds, our algorithm achieves $\widetilde{O}((d_1+d_2)^{3/2}\sqrt{rT})$ regret that improves upon the standard linear bandit regret bound of $\widetilde{O}(d_1d_2\sqrt{T})$ when the rank of $\Theta^*$: $r \ll \min\{d_1,d_2\}$. We also extend our algorithmic approach to the generalized linear setting to get an algorithm which enjoys a similar bound under regularity conditions on the link function. To get around the computational intractability of covering based approaches, we propose an efficient algorithm by extending the "Explore-Subspace-Then-Refine" algorithm of~\citet{jun2019bilinear}. Our efficient algorithm achieves $\widetilde{O}((d_1+d_2)^{3/2}\sqrt{rT})$ regret under a mild condition on the action set $\mathcal{X}$ and the $r$-th singular value of $\Theta^*$. Our upper bounds match the conjectured lower bound of \cite{jun2019bilinear} for a subclass of low-rank linear bandit problems. Further, we show that existing lower bounds for the sparse linear bandit problem strongly suggest that our regret bounds are unimprovable. To complement our theoretical contributions, we also conduct experiments to demonstrate that our algorithm can greatly outperform the performance of the standard linear bandit approach when $\Theta^*$ is low-rank.

Regret Analysis of Causal Bandit Problems

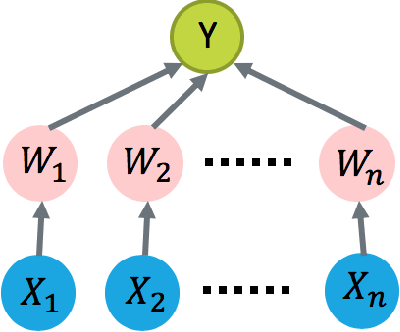
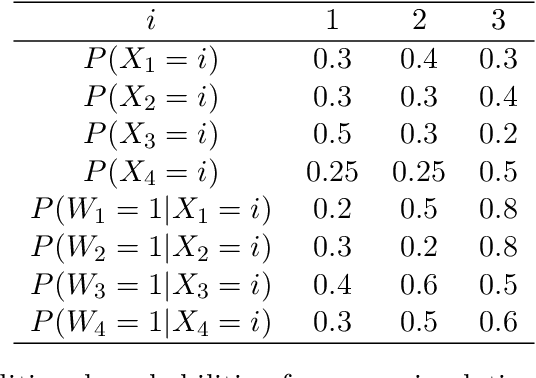
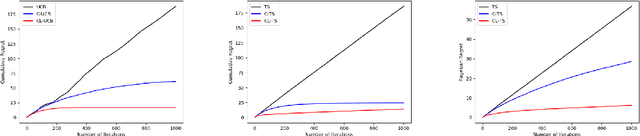
We study how to learn optimal interventions sequentially given causal information represented as a causal graph along with associated conditional distributions. Causal modeling is useful in real world problems like online advertisement where complex causal mechanisms underlie the relationship between interventions and outcomes. We propose two algorithms, causal upper confidence bound (C-UCB) and causal Thompson Sampling (C-TS), that enjoy improved cumulative regret bounds compared with algorithms that do not use causal information. We thus resolve an open problem posed by~\cite{lattimore2016causal}. Further, we extend C-UCB and C-TS to the linear bandit setting and propose causal linear UCB (CL-UCB) and causal linear TS (CL-TS) algorithms. These algorithms enjoy a cumulative regret bound that only scales with the feature dimension. Our experiments show the benefit of using causal information. For example, we observe that even with a few hundreds of iterations, the regret of causal algorithms is less than that of standard algorithms by a factor of three. We also show that under certain causal structures, our algorithms scale better than the standard bandit algorithms as the number of interventions increases.