Causal Markov Decision Processes: Learning Good Interventions Efficiently
Paper and Code
Feb 15, 2021
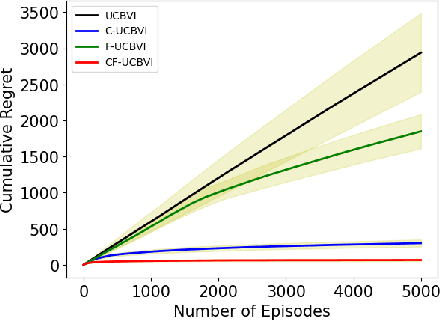
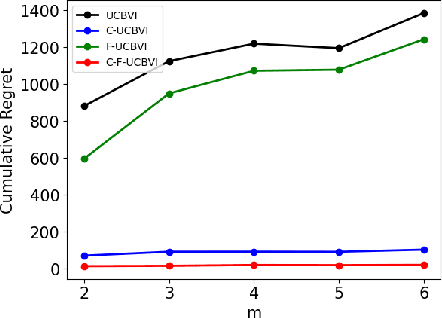
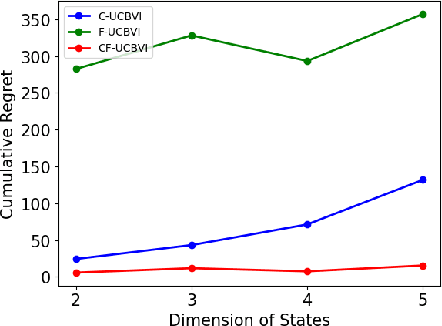
We introduce causal Markov Decision Processes (C-MDPs), a new formalism for sequential decision making which combines the standard MDP formulation with causal structures over state transition and reward functions. Many contemporary and emerging application areas such as digital healthcare and digital marketing can benefit from modeling with C-MDPs due to the causal mechanisms underlying the relationship between interventions and states/rewards. We propose the causal upper confidence bound value iteration (C-UCBVI) algorithm that exploits the causal structure in C-MDPs and improves the performance of standard reinforcement learning algorithms that do not take causal knowledge into account. We prove that C-UCBVI satisfies an $\tilde{O}(HS\sqrt{ZT})$ regret bound, where $T$ is the the total time steps, $H$ is the episodic horizon, and $S$ is the cardinality of the state space. Notably, our regret bound does not scale with the size of actions/interventions ($A$), but only scales with a causal graph dependent quantity $Z$ which can be exponentially smaller than $A$. By extending C-UCBVI to the factored MDP setting, we propose the causal factored UCBVI (CF-UCBVI) algorithm, which further reduces the regret exponentially in terms of $S$. Furthermore, we show that RL algorithms for linear MDP problems can also be incorporated in C-MDPs. We empirically show the benefit of our causal approaches in various settings to validate our algorithms and theoretical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge