Amirhossein Meisami
A Graphical Point Process Framework for Understanding Removal Effects in Multi-Touch Attribution
Feb 13, 2023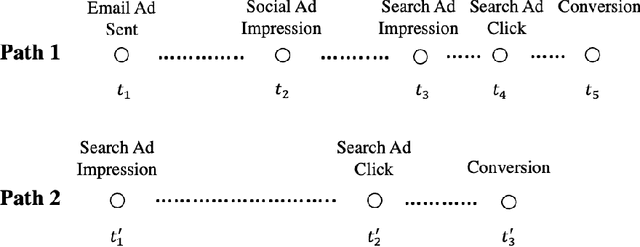

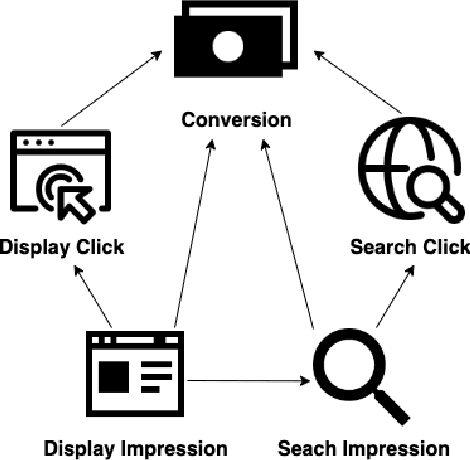
Abstract:Marketers employ various online advertising channels to reach customers, and they are particularly interested in attribution for measuring the degree to which individual touchpoints contribute to an eventual conversion. The availability of individual customer-level path-to-purchase data and the increasing number of online marketing channels and types of touchpoints bring new challenges to this fundamental problem. We aim to tackle the attribution problem with finer granularity by conducting attribution at the path level. To this end, we develop a novel graphical point process framework to study the direct conversion effects and the full relational structure among numerous types of touchpoints simultaneously. Utilizing the temporal point process of conversion and the graphical structure, we further propose graphical attribution methods to allocate proper path-level conversion credit, called the attribution score, to individual touchpoints or corresponding channels for each customer's path to purchase. Our proposed attribution methods consider the attribution score as the removal effect, and we use the rigorous probabilistic definition to derive two types of removal effects. We examine the performance of our proposed methods in extensive simulation studies and compare their performance with commonly used attribution models. We also demonstrate the performance of the proposed methods in a real-world attribution application.
Generalized Bayesian Upper Confidence Bound with Approximate Inference for Bandit Problems
Jan 31, 2022



Abstract:Bayesian bandit algorithms with approximate inference have been widely used in practice with superior performance. Yet, few studies regarding the fundamental understanding of their performances are available. In this paper, we propose a Bayesian bandit algorithm, which we call Generalized Bayesian Upper Confidence Bound (GBUCB), for bandit problems in the presence of approximate inference. Our theoretical analysis demonstrates that in Bernoulli multi-armed bandit, GBUCB can achieve $O(\sqrt{T}(\log T)^c)$ frequentist regret if the inference error measured by symmetrized Kullback-Leibler divergence is controllable. This analysis relies on a novel sensitivity analysis for quantile shifts with respect to inference errors. To our best knowledge, our work provides the first theoretical regret bound that is better than $o(T)$ in the setting of approximate inference. Our experimental evaluations on multiple approximate inference settings corroborate our theory, showing that our GBUCB is consistently superior to BUCB and Thompson sampling.
Causal Bandits with Unknown Graph Structure
Jun 05, 2021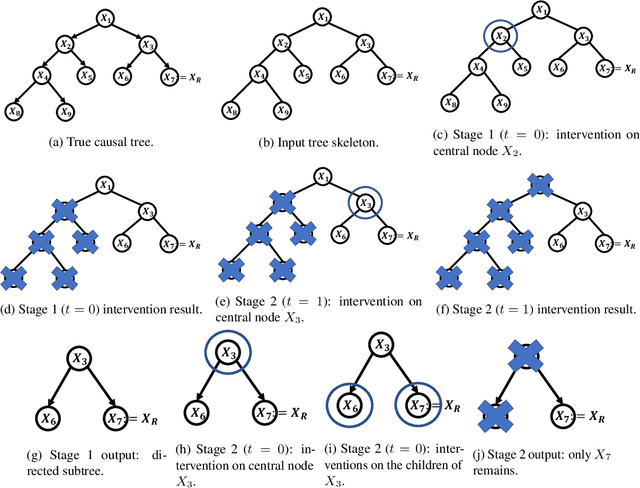
Abstract:In causal bandit problems, the action set consists of interventions on variables of a causal graph. Several researchers have recently studied such bandit problems and pointed out their practical applications. However, all existing works rely on a restrictive and impractical assumption that the learner is given full knowledge of the causal graph structure upfront. In this paper, we develop novel causal bandit algorithms without knowing the causal graph. Our algorithms work well for causal trees, causal forests and a general class of causal graphs. The regret guarantees of our algorithms greatly improve upon those of standard multi-armed bandit (MAB) algorithms under mild conditions. Lastly, we prove our mild conditions are necessary: without them one cannot do better than standard MAB bandit algorithms.
Causal Markov Decision Processes: Learning Good Interventions Efficiently
Feb 15, 2021
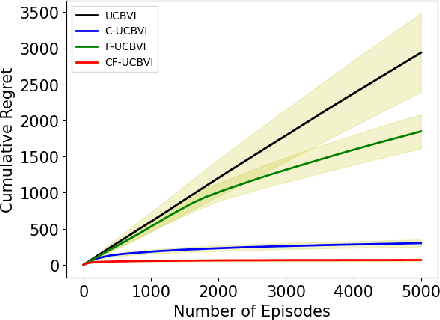
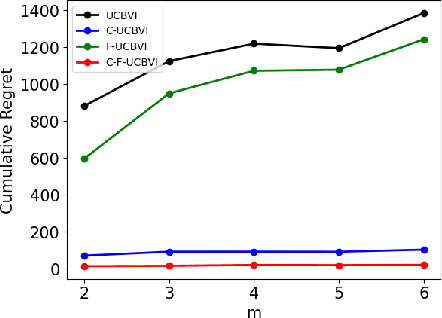
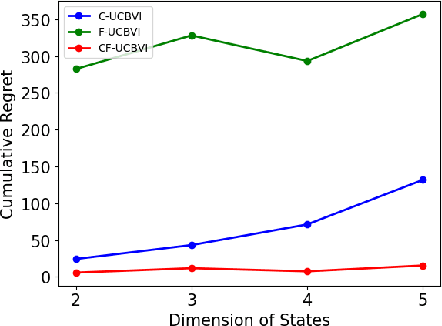
Abstract:We introduce causal Markov Decision Processes (C-MDPs), a new formalism for sequential decision making which combines the standard MDP formulation with causal structures over state transition and reward functions. Many contemporary and emerging application areas such as digital healthcare and digital marketing can benefit from modeling with C-MDPs due to the causal mechanisms underlying the relationship between interventions and states/rewards. We propose the causal upper confidence bound value iteration (C-UCBVI) algorithm that exploits the causal structure in C-MDPs and improves the performance of standard reinforcement learning algorithms that do not take causal knowledge into account. We prove that C-UCBVI satisfies an $\tilde{O}(HS\sqrt{ZT})$ regret bound, where $T$ is the the total time steps, $H$ is the episodic horizon, and $S$ is the cardinality of the state space. Notably, our regret bound does not scale with the size of actions/interventions ($A$), but only scales with a causal graph dependent quantity $Z$ which can be exponentially smaller than $A$. By extending C-UCBVI to the factored MDP setting, we propose the causal factored UCBVI (CF-UCBVI) algorithm, which further reduces the regret exponentially in terms of $S$. Furthermore, we show that RL algorithms for linear MDP problems can also be incorporated in C-MDPs. We empirically show the benefit of our causal approaches in various settings to validate our algorithms and theoretical results.
Low-Rank Generalized Linear Bandit Problems
Jun 04, 2020

Abstract:In a low-rank linear bandit problem, the reward of an action (represented by a matrix of size $d_1 \times d_2$) is the inner product between the action and an unknown low-rank matrix $\Theta^*$. We propose an algorithm based on a novel combination of online-to-confidence-set conversion~\citep{abbasi2012online} and the exponentially weighted average forecaster constructed by a covering of low-rank matrices. In $T$ rounds, our algorithm achieves $\widetilde{O}((d_1+d_2)^{3/2}\sqrt{rT})$ regret that improves upon the standard linear bandit regret bound of $\widetilde{O}(d_1d_2\sqrt{T})$ when the rank of $\Theta^*$: $r \ll \min\{d_1,d_2\}$. We also extend our algorithmic approach to the generalized linear setting to get an algorithm which enjoys a similar bound under regularity conditions on the link function. To get around the computational intractability of covering based approaches, we propose an efficient algorithm by extending the "Explore-Subspace-Then-Refine" algorithm of~\citet{jun2019bilinear}. Our efficient algorithm achieves $\widetilde{O}((d_1+d_2)^{3/2}\sqrt{rT})$ regret under a mild condition on the action set $\mathcal{X}$ and the $r$-th singular value of $\Theta^*$. Our upper bounds match the conjectured lower bound of \cite{jun2019bilinear} for a subclass of low-rank linear bandit problems. Further, we show that existing lower bounds for the sparse linear bandit problem strongly suggest that our regret bounds are unimprovable. To complement our theoretical contributions, we also conduct experiments to demonstrate that our algorithm can greatly outperform the performance of the standard linear bandit approach when $\Theta^*$ is low-rank.
Regret Analysis of Causal Bandit Problems
Oct 11, 2019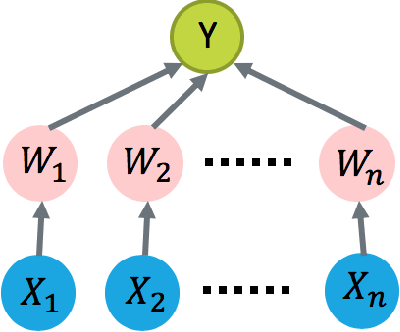
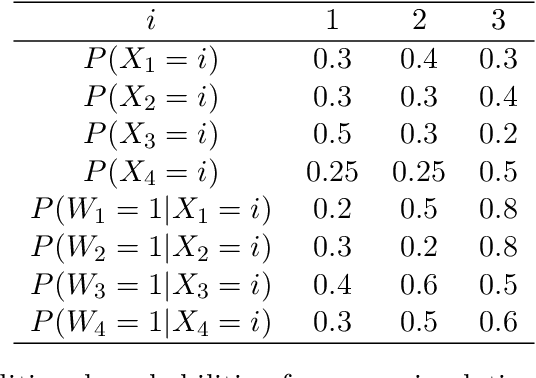
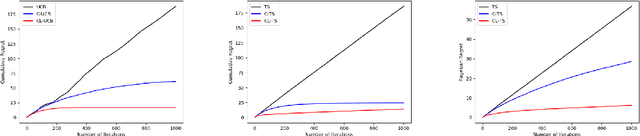

Abstract:We study how to learn optimal interventions sequentially given causal information represented as a causal graph along with associated conditional distributions. Causal modeling is useful in real world problems like online advertisement where complex causal mechanisms underlie the relationship between interventions and outcomes. We propose two algorithms, causal upper confidence bound (C-UCB) and causal Thompson Sampling (C-TS), that enjoy improved cumulative regret bounds compared with algorithms that do not use causal information. We thus resolve an open problem posed by~\cite{lattimore2016causal}. Further, we extend C-UCB and C-TS to the linear bandit setting and propose causal linear UCB (CL-UCB) and causal linear TS (CL-TS) algorithms. These algorithms enjoy a cumulative regret bound that only scales with the feature dimension. Our experiments show the benefit of using causal information. For example, we observe that even with a few hundreds of iterations, the regret of causal algorithms is less than that of standard algorithms by a factor of three. We also show that under certain causal structures, our algorithms scale better than the standard bandit algorithms as the number of interventions increases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge