Yangbin Lin
Quantum Complex-Valued Self-Attention Model
Mar 24, 2025Abstract:The self-attention mechanism has revolutionized classical machine learning, yet its quantum counterpart remains underexplored in fully harnessing the representational power of quantum states. Current quantum self-attention models exhibit a critical limitation by neglecting the indispensable phase information inherent in quantum systems when compressing attention weights into real-valued overlaps. To address this fundamental gap, we propose the Quantum Complex-Valued Self-Attention Model (QCSAM), the first framework that explicitly leverages complex-valued similarities between quantum states to capture both amplitude and phase relationships. Simultaneously, we enhance the standard Linear Combination of Unitaries (LCUs) method by introducing a Complex LCUs (CLCUs) framework that natively supports complex-valued coefficients. This framework enables the weighting of corresponding quantum values using fixed quantum complex self-attention weights, while also supporting trainable complex-valued parameters for value aggregation and quantum multi-head attention. Experimental evaluations on MNIST and Fashion-MNIST demonstrate our model's superiority over recent quantum self-attention architectures including QKSAN, QSAN, and GQHAN, with multi-head configurations showing consistent advantages over single-head variants. We systematically evaluate model scalability through qubit configurations ranging from 3 to 8 qubits and multi-class classification tasks spanning 2 to 4 categories. Through comprehensive ablation studies, we establish the critical advantage of complex-valued quantum attention weights over real-valued alternatives.
Quantum Mixed-State Self-Attention Network
Mar 05, 2024



Abstract:The rapid advancement of quantum computing has increasingly highlighted its potential in the realm of machine learning, particularly in the context of natural language processing (NLP) tasks. Quantum machine learning (QML) leverages the unique capabilities of quantum computing to offer novel perspectives and methodologies for complex data processing and pattern recognition challenges. This paper introduces a novel Quantum Mixed-State Attention Network (QMSAN), which integrates the principles of quantum computing with classical machine learning algorithms, especially self-attention networks, to enhance the efficiency and effectiveness in handling NLP tasks. QMSAN model employs a quantum attention mechanism based on mixed states, enabling efficient direct estimation of similarity between queries and keys within the quantum domain, leading to more effective attention weight acquisition. Additionally, we propose an innovative quantum positional encoding scheme, implemented through fixed quantum gates within the quantum circuit, to enhance the model's accuracy. Experimental validation on various datasets demonstrates that QMSAN model outperforms existing quantum and classical models in text classification, achieving significant performance improvements. QMSAN model not only significantly reduces the number of parameters but also exceeds classical self-attention networks in performance, showcasing its strong capability in data representation and information extraction. Furthermore, our study investigates the model's robustness in different quantum noise environments, showing that QMSAN possesses commendable robustness to low noise.
Fast Regularity-Constrained Plane Reconstruction
May 20, 2019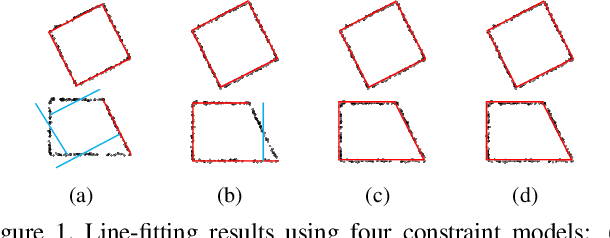
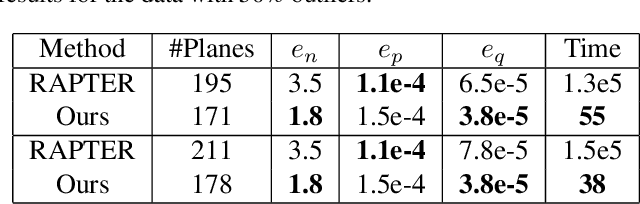
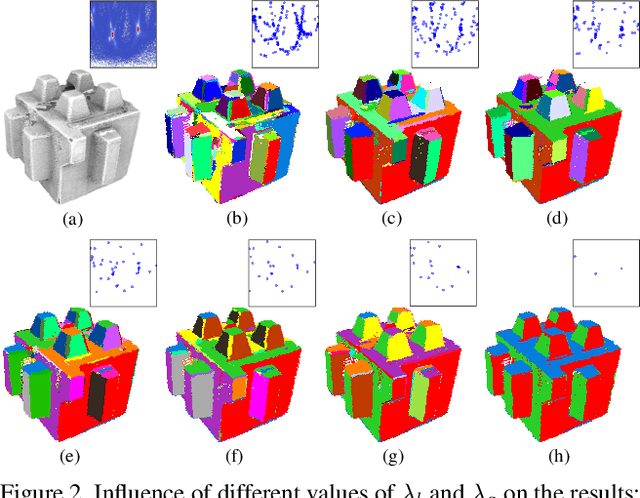
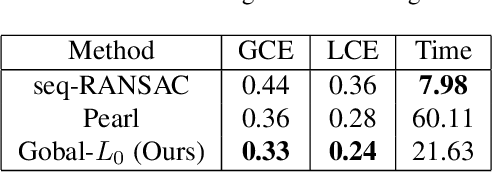
Abstract:Man-made environments typically comprise planar structures that exhibit numerous geometric relationships, such as parallelism, coplanarity, and orthogonality. Making full use of these relationships can considerably improve the robustness of algorithmic plane reconstruction of complex scenes. This research leverages a constraint model requiring minimal prior knowledge to implicitly establish relationships among planes. We introduce a method based on energy minimization to reconstruct the planes consistent with our constraint model. The proposed algorithm is efficient, easily to understand, and simple to implement. The experimental results show that our algorithm successfully reconstructs planes under high percentages of noise and outliers. This is superior to other state-of-the-art regularity-constrained plane reconstruction methods in terms of speed and robustness.
Partial Procedural Geometric Model Fitting for Point Clouds
Oct 17, 2016



Abstract:Geometric model fitting is a fundamental task in computer graphics and computer vision. However, most geometric model fitting methods are unable to fit an arbitrary geometric model (e.g. a surface with holes) to incomplete data, due to that the similarity metrics used in these methods are unable to measure the rigid partial similarity between arbitrary models. This paper hence proposes a novel rigid geometric similarity metric, which is able to measure both the full similarity and the partial similarity between arbitrary geometric models. The proposed metric enables us to perform partial procedural geometric model fitting (PPGMF). The task of PPGMF is to search a procedural geometric model space for the model rigidly similar to a query of non-complete point set. Models in the procedural model space are generated according to a set of parametric modeling rules. A typical query is a point cloud. PPGMF is very useful as it can be used to fit arbitrary geometric models to non-complete (incomplete, over-complete or hybrid-complete) point cloud data. For example, most laser scanning data is non-complete due to occlusion. Our PPGMF method uses Markov chain Monte Carlo technique to optimize the proposed similarity metric over the model space. To accelerate the optimization process, the method also employs a novel coarse-to-fine model dividing strategy to reject dissimilar models in advance. Our method has been demonstrated on a variety of geometric models and non-complete data. Experimental results show that the PPGMF method based on the proposed metric is able to fit non-complete data, while the method based on other metrics is unable. It is also shown that our method can be accelerated by several times via early rejection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge