Xue-cheng Tai
Department of Mathematics, Hong Kong Baptist University, China
IDmUNet: A new image decomposition induced network for sparse feature segmentation
Mar 05, 2022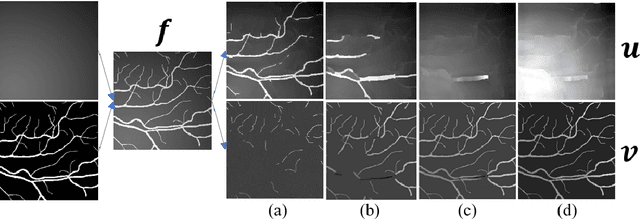
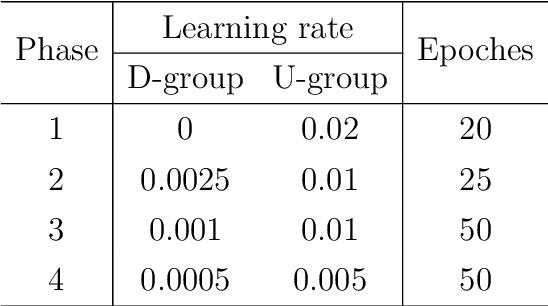
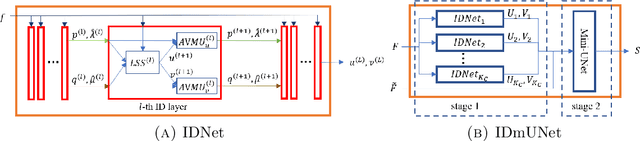
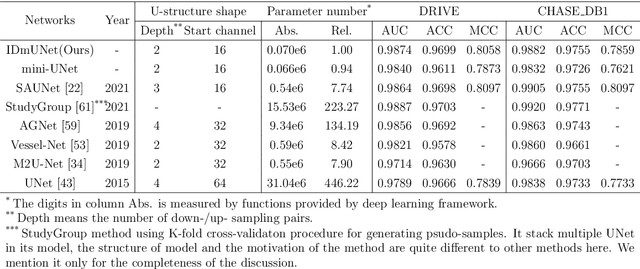
Abstract:UNet and its variants are among the most popular methods for medical image segmentation. Despite their successes in task generality, most of them consider little mathematical modeling behind specific applications. In this paper, we focus on the sparse feature segmentation task and make a task-oriented network design, in which the target objects are sparsely distributed and the background is hard to be mathematically modeled. We start from an image decomposition model with sparsity regularization, and propose a deep unfolding network, namely IDNet, based on an iterative solver, scaled alternating direction method of multipliers (scaled-ADMM). The IDNet splits raw inputs into double feature layers. Then a new task-oriented segmentation network is constructed, dubbed as IDmUNet, based on the proposed IDNets and a mini-UNet. Because of the sparsity prior and deep unfolding method in the structure design, this IDmUNet combines the advantages of mathematical modeling and data-driven approaches. Firstly, our approach has mathematical interpretability and can achieve favorable performance with far fewer learnable parameters. Secondly, our IDmUNet is robust in a simple end-to-end training with explainable behaviors. In the experiments of retinal vessel segmentation (RVS), IDmUNet produces the state-of-the-art results with only 0.07m parameters, whereas SA-UNet, one of the latest variants of UNet, contains 0.54m and the original UNet 31.04m. Moreover, the training procedure of our network converges faster without overfitting phenomenon. This decomposition-based network construction strategy can be generalized to other problems with mathematically clear targets and complicated unclear backgrounds.
Deep Convolutional Neural Networks with Spatial Regularization, Volume and Star-shape Priori for Image Segmentation
Feb 10, 2020



Abstract:We use Deep Convolutional Neural Networks (DCNNs) for image segmentation problems. DCNNs can well extract the features from natural images. However, the classification functions in the existing network architecture of CNNs are simple and lack capabilities to handle important spatial information in a way that have been done for many well-known traditional variational models. Prior such as spatial regularity, volume prior and object shapes cannot be well handled by existing DCNNs. We propose a novel Soft Threshold Dynamics (STD) framework which can easily integrate many spatial priors of the classical variational models into the DCNNs for image segmentation. The novelty of our method is to interpret the softmax activation function as a dual variable in a variational problem, and thus many spatial priors can be imposed in the dual space. From this viewpoint, we can build a STD based framework which can enable the outputs of DCNNs to have many special priors such as spatial regularity, volume constraints and star-shape priori. The proposed method is a general mathematical framework and it can be applied to any semantic segmentation DCNNs. To show the efficiency and accuracy of our method, we applied it to the popular DeepLabV3+ image segmentation network, and the experiments results show that our method can work efficiently on data-driven image segmentation DCNNs.
Volume Preserving Image Segmentation with Entropic Regularization Optimal Transport and Its Applications in Deep Learning
Sep 22, 2019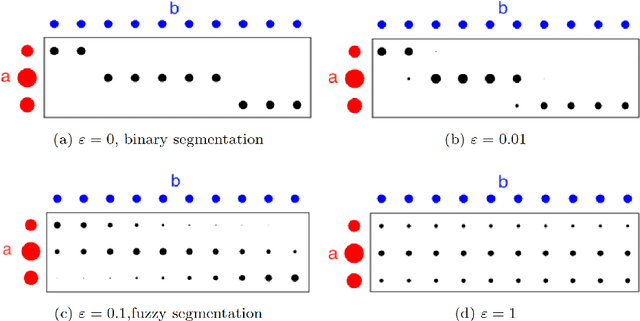
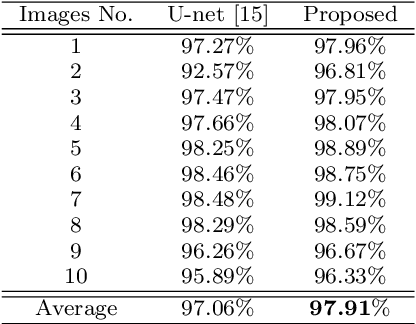
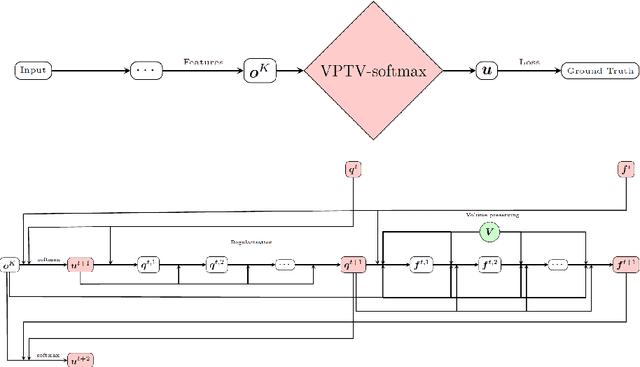
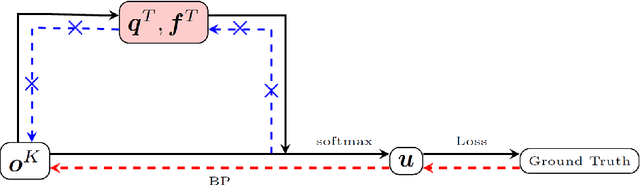
Abstract:Image segmentation with a volume constraint is an important prior for many real applications. In this work, we present a novel volume preserving image segmentation algorithm, which is based on the framework of entropic regularized optimal transport theory. The classical Total Variation (TV) regularizer and volume preserving are integrated into a regularized optimal transport model, and the volume and classification constraints can be regarded as two measures preserving constraints in the optimal transport problem. By studying the dual problem, we develop a simple and efficient dual algorithm for our model. Moreover, to be different from many variational based image segmentation algorithms, the proposed algorithm can be directly unrolled to a new Volume Preserving and TV regularized softmax (VPTV-softmax) layer for semantic segmentation in the popular Deep Convolution Neural Network (DCNN). The experiment results show that our proposed model is very competitive and can improve the performance of many semantic segmentation nets such as the popular U-net.
A Regularized Convolutional Neural Network for Semantic Image Segmentation
Jun 28, 2019



Abstract:Convolutional neural networks (CNNs) show outstanding performance in many image processing problems, such as image recognition, object detection and image segmentation. Semantic segmentation is a very challenging task that requires recognizing, understanding what's in the image in pixel level. Though the state of the art has been greatly improved by CNNs, there is no explicit connections between prediction of neighbouring pixels. That is, spatial regularity of the segmented objects is still a problem for CNNs. In this paper, we propose a method to add spatial regularization to the segmented objects. In our method, the spatial regularization such as total variation (TV) can be easily integrated into CNN network. It can help CNN find a better local optimum and make the segmentation results more robust to noise. We apply our proposed method to Unet and Segnet, which are well established CNNs for image segmentation, and test them on WBC, CamVid and SUN-RGBD datasets, respectively. The results show that the regularized networks not only could provide better segmentation results with regularization effect than the original ones but also have certain robustness to noise.
Convexity Shape Prior for Level Set based Image Segmentation Method
May 22, 2018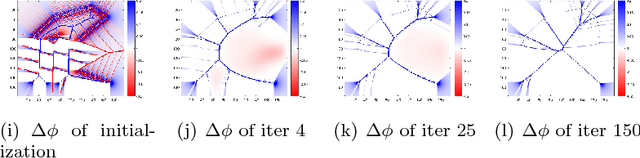
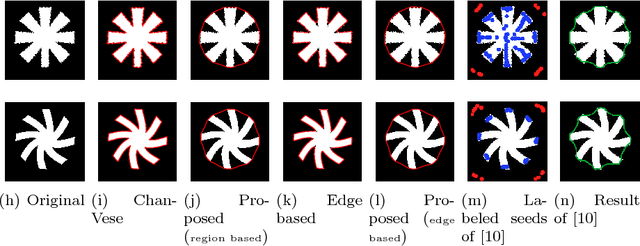
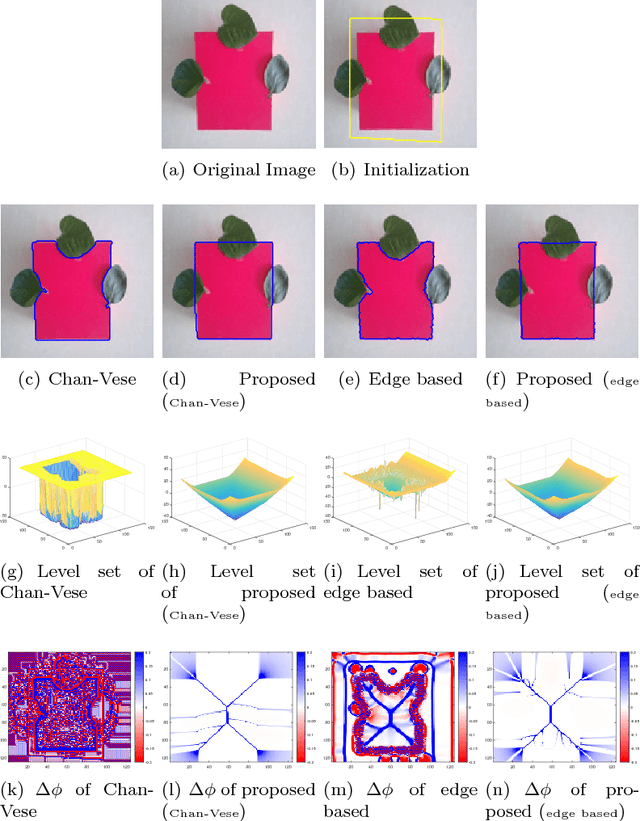

Abstract:We propose a geometric convexity shape prior preservation method for variational level set based image segmentation methods. Our method is built upon the fact that the level set of a convex signed distanced function must be convex. This property enables us to transfer a complicated geometrical convexity prior into a simple inequality constraint on the function. An active set based Gauss-Seidel iteration is used to handle this constrained minimization problem to get an efficient algorithm. We apply our method to region and edge based level set segmentation models including Chan-Vese (CV) model with guarantee that the segmented region will be convex. Experimental results show the effectiveness and quality of the proposed model and algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge