Mathematical Modeling and Convergence Analysis of Deep Neural Networks with Dense Layer Connectivities in Deep Learning

In deep learning, dense layer connectivity has become a key design principle in deep neural networks (DNNs), enabling efficient information flow and strong performance across a range of applications. In this work, we model densely connected DNNs mathematically and analyze their learning problems in the deep-layer limit. For a broad applicability, we present our analysis in a framework setting of DNNs with densely connected layers and general non-local feature transformations (with local feature transformations as special cases) within layers, which is called dense non-local (DNL) framework and includes standard DenseNets and variants as special examples. In this formulation, the densely connected networks are modeled as nonlinear integral equations, in contrast to the ordinary differential equation viewpoint commonly adopted in prior works. We study the associated training problems from an optimal control perspective and prove convergence results from the network learning problem to its continuous-time counterpart. In particular, we show the convergence of optimal values and the subsequence convergence of minimizers, using a piecewise linear extension and $\Gamma$-convergence analysis. Our results provide a mathematical foundation for understanding densely connected DNNs and further suggest that such architectures can offer stability of training deep models.

IDmUNet: A new image decomposition induced network for sparse feature segmentation

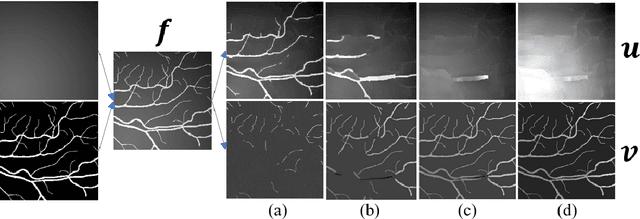
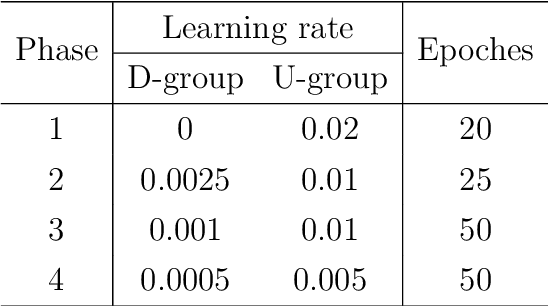
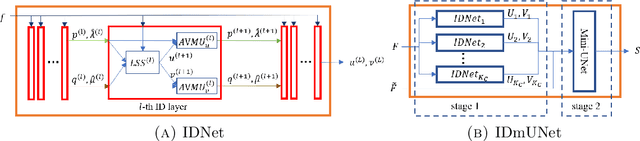
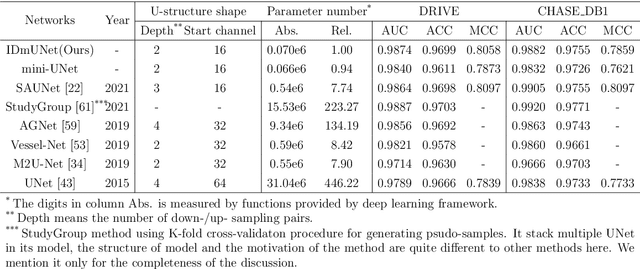
UNet and its variants are among the most popular methods for medical image segmentation. Despite their successes in task generality, most of them consider little mathematical modeling behind specific applications. In this paper, we focus on the sparse feature segmentation task and make a task-oriented network design, in which the target objects are sparsely distributed and the background is hard to be mathematically modeled. We start from an image decomposition model with sparsity regularization, and propose a deep unfolding network, namely IDNet, based on an iterative solver, scaled alternating direction method of multipliers (scaled-ADMM). The IDNet splits raw inputs into double feature layers. Then a new task-oriented segmentation network is constructed, dubbed as IDmUNet, based on the proposed IDNets and a mini-UNet. Because of the sparsity prior and deep unfolding method in the structure design, this IDmUNet combines the advantages of mathematical modeling and data-driven approaches. Firstly, our approach has mathematical interpretability and can achieve favorable performance with far fewer learnable parameters. Secondly, our IDmUNet is robust in a simple end-to-end training with explainable behaviors. In the experiments of retinal vessel segmentation (RVS), IDmUNet produces the state-of-the-art results with only 0.07m parameters, whereas SA-UNet, one of the latest variants of UNet, contains 0.54m and the original UNet 31.04m. Moreover, the training procedure of our network converges faster without overfitting phenomenon. This decomposition-based network construction strategy can be generalized to other problems with mathematically clear targets and complicated unclear backgrounds.

A fast method for simultaneous reconstruction and segmentation in X-ray CT application

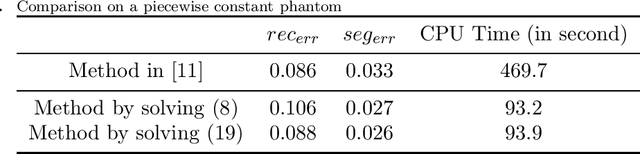
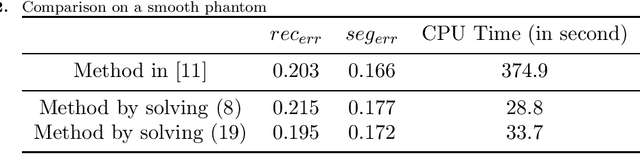
In this paper, we propose a fast method for simultaneous reconstruction and segmentation (SRS) in X-ray computed tomography (CT). Our work is based on the SRS model where Bayes' rule and the maximum a posteriori (MAP) are used on hidden Markov measure field model (HMMFM). The original method leads to a logarithmic-summation (log-sum) term, which is non-separable to the classification index. The minimization problem in the model was solved by using constrained gradient descend method, Frank-Wolfe algorithm, which is very time-consuming especially when dealing with large-scale CT problems. The starting point of this paper is the commutativity of log-sum operations, where the log-sum problem could be transformed into a sum-log problem by introducing an auxiliary variable. The corresponding sum-log problem for the SRS model is separable. After applying alternating minimization method, this problem turns into several easy-to-solve convex sub-problems. In the paper, we also study an improved model by adding Tikhonov regularization, and give some convergence results. Experimental results demonstrate that the proposed algorithms could produce comparable results with the original SRS method with much less CPU time.

The Continuity of Images by Transmission Imaging Revisited

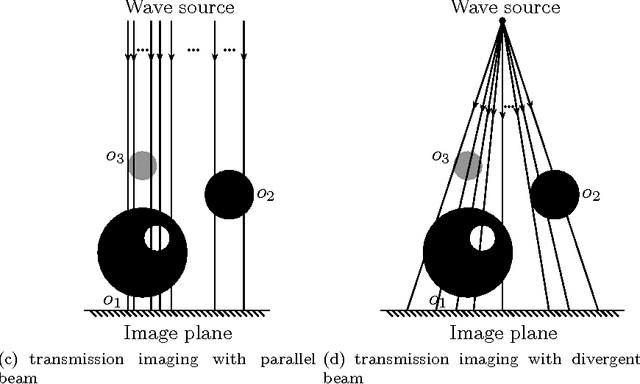
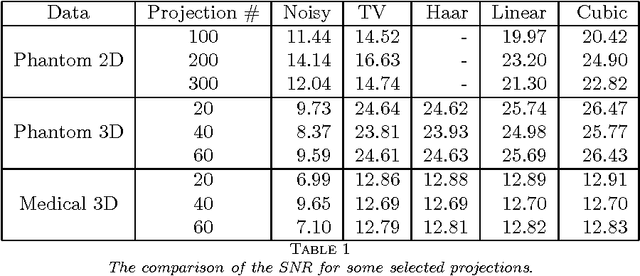
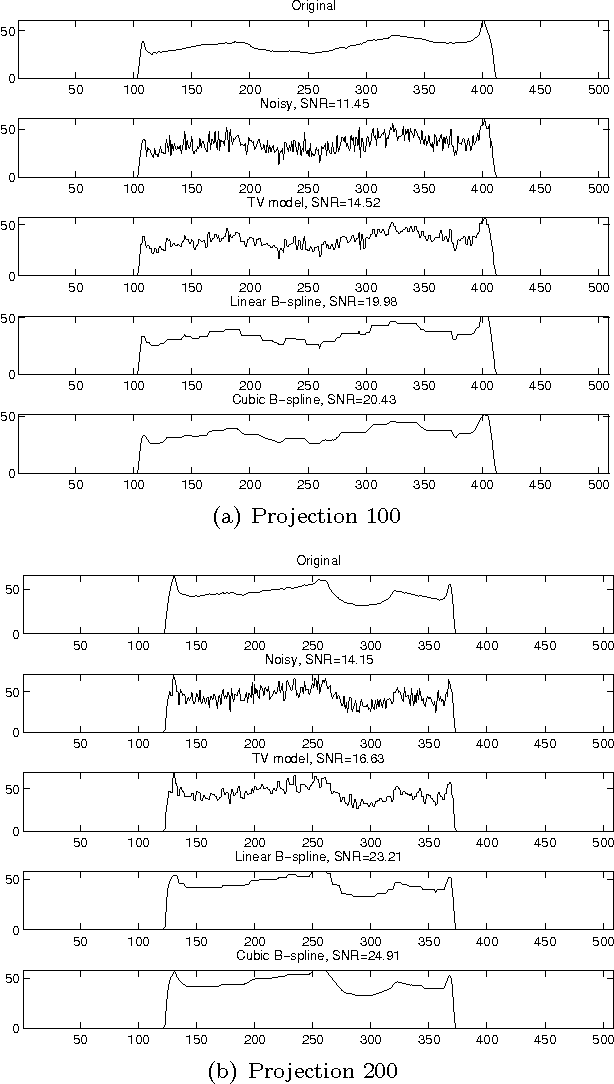
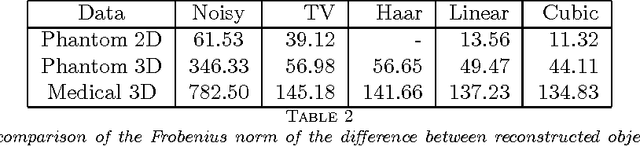
Transmission imaging, as an important imaging technique widely used in astronomy, medical diagnosis, and biology science, has been shown in [49] quite different from reflection imaging used in our everyday life. Understanding the structures of images (the prior information) is important for designing, testing, and choosing image processing methods, and good image processing methods are helpful for further uses of the image data, e.g., increasing the accuracy of the object reconstruction methods in transmission imaging applications. In reflection imaging, the images are usually modeled as discontinuous functions and even piecewise constant functions. In transmission imaging, it was shown very recently in [49] that almost all images are continuous functions. However, the author in [49] considered only the case of parallel beam geometry and used some too strong assumptions in the proof, which exclude some common cases such as cylindrical objects. In this paper, we consider more general beam geometries and simplify the assumptions by using totally different techniques. In particular, we will prove that almost all images in transmission imaging with both parallel and divergent beam geometries (two most typical beam geometries) are continuous functions, under much weaker assumptions than those in [49], which admit almost all practical cases. Besides, taking into accounts our analysis, we compare two image processing methods for Poisson noise (which is the most significant noise in transmission imaging) removal. Numerical experiments will be provided to demonstrate our analysis.