The Continuity of Images by Transmission Imaging Revisited
Paper and Code
Jan 08, 2014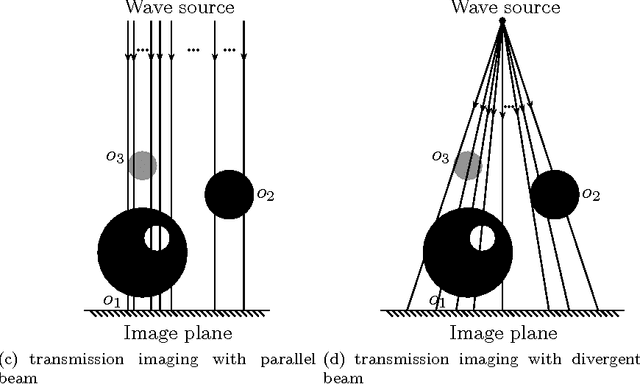
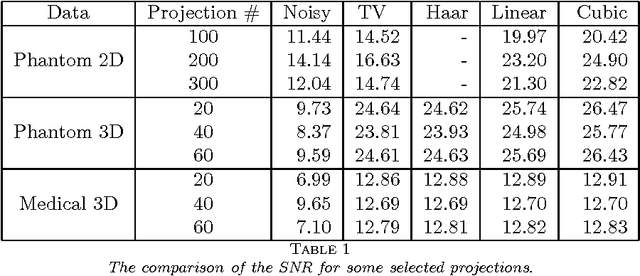
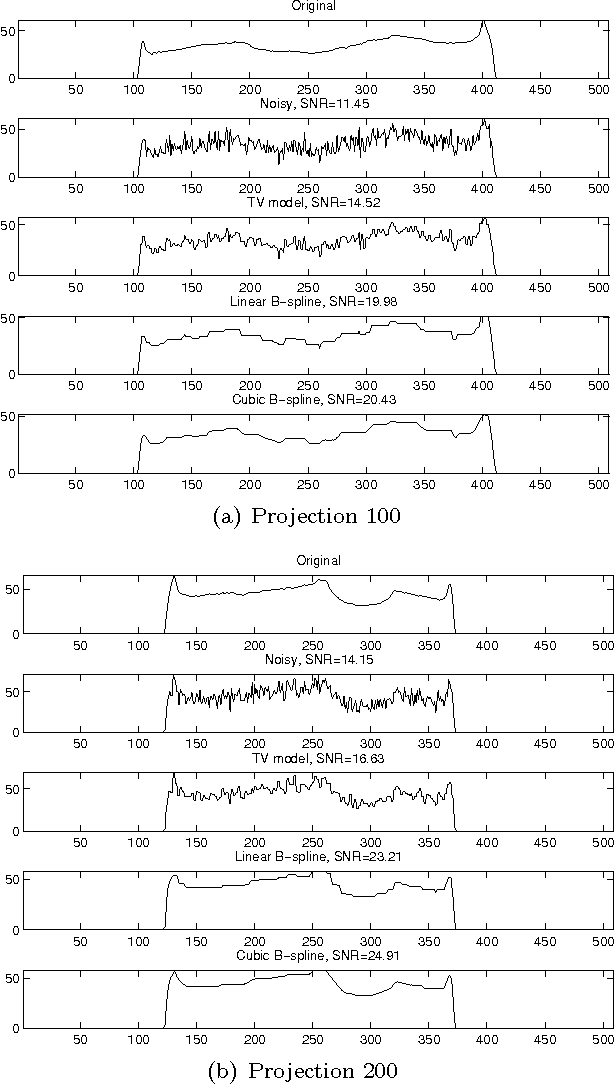
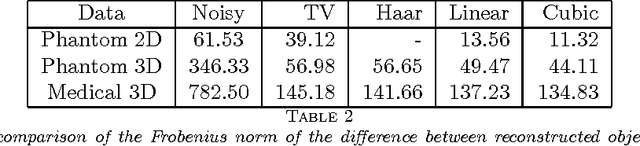
Transmission imaging, as an important imaging technique widely used in astronomy, medical diagnosis, and biology science, has been shown in [49] quite different from reflection imaging used in our everyday life. Understanding the structures of images (the prior information) is important for designing, testing, and choosing image processing methods, and good image processing methods are helpful for further uses of the image data, e.g., increasing the accuracy of the object reconstruction methods in transmission imaging applications. In reflection imaging, the images are usually modeled as discontinuous functions and even piecewise constant functions. In transmission imaging, it was shown very recently in [49] that almost all images are continuous functions. However, the author in [49] considered only the case of parallel beam geometry and used some too strong assumptions in the proof, which exclude some common cases such as cylindrical objects. In this paper, we consider more general beam geometries and simplify the assumptions by using totally different techniques. In particular, we will prove that almost all images in transmission imaging with both parallel and divergent beam geometries (two most typical beam geometries) are continuous functions, under much weaker assumptions than those in [49], which admit almost all practical cases. Besides, taking into accounts our analysis, we compare two image processing methods for Poisson noise (which is the most significant noise in transmission imaging) removal. Numerical experiments will be provided to demonstrate our analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge