Rapid Assessments of Light-Duty Gasoline Vehicle Emissions Using On-Road Remote Sensing and Machine Learning

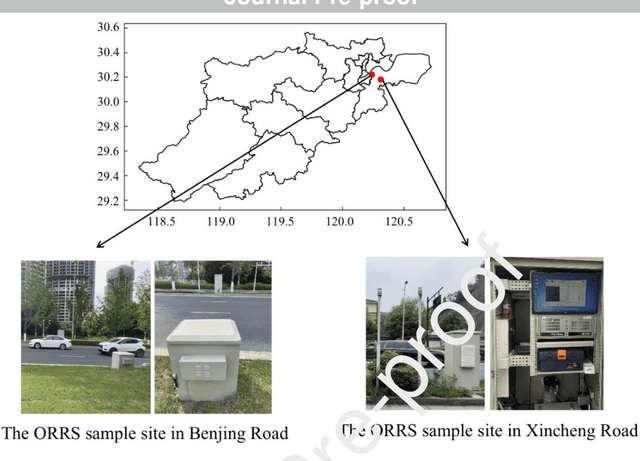
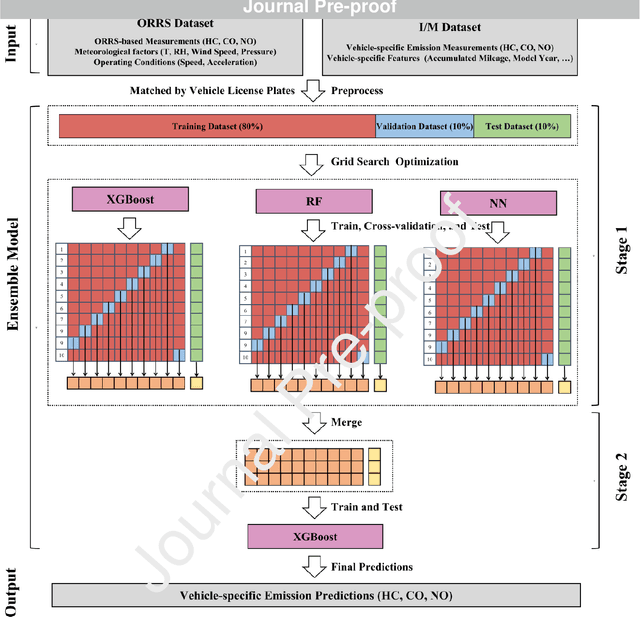
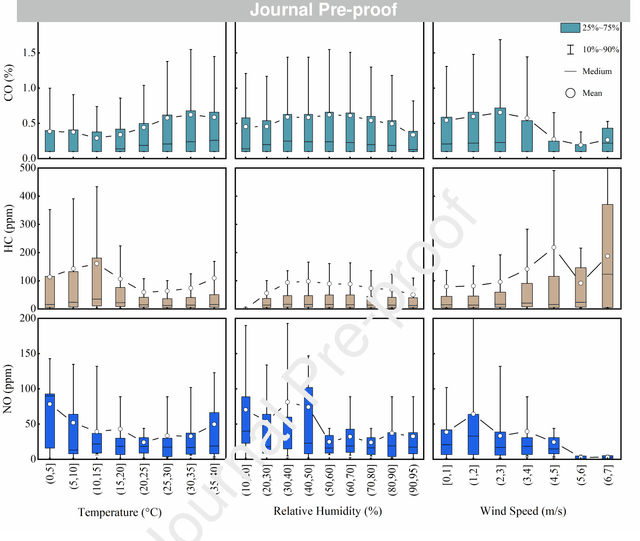
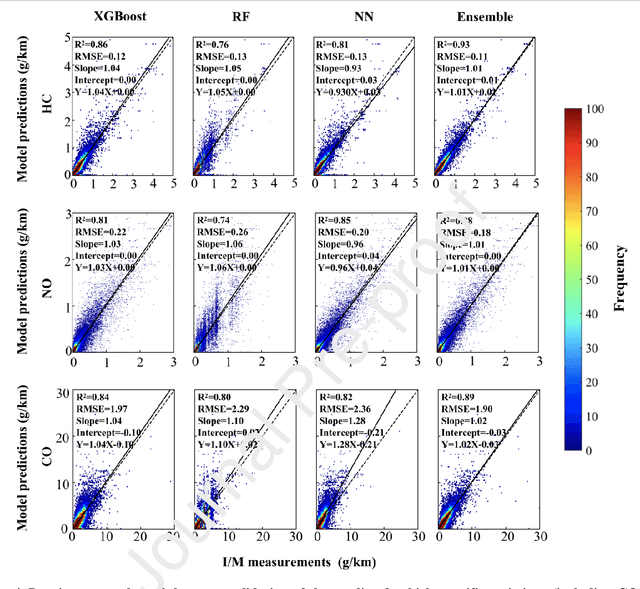
In-time and accurate assessments of on-road vehicle emissions play a central role in urban air quality and health policymaking. However, official insight is hampered by the Inspection/Maintenance (I/M) procedure conducted in the laboratory annually. It not only has a large gap to real-world situations (e.g., meteorological conditions) but also is incapable of regular supervision. Here we build a unique dataset including 103831 light-duty gasoline vehicles, in which on-road remote sensing (ORRS) measurements are linked to the I/M records based on the vehicle identification numbers and license plates. On this basis, we develop an ensemble model framework that integrates three machining learning algorithms, including neural network (NN), extreme gradient boosting (XGBoost), and random forest (RF). We demonstrate that this ensemble model could rapidly assess the vehicle-specific emissions (i.e., CO, HC, and NO). In particular, the model performs quite well for the passing vehicles under normal conditions (i.e., lower VSP (< 18 kw/t), temperature (6 ~ 32 {\deg}C), relative humidity (< 80%), and wind speed (< 5m/s)). Together with the current emission standard, we identify a large number of the dirty (2.33%) or clean (74.92%) vehicles in the real world. Our results show that the ORRS measurements, assisted by the machine-learning-based ensemble model developed here, can realize day-to-day supervision of on-road vehicle-specific emissions. This approach framework provides a valuable opportunity to reform the I/M procedures globally and mitigate urban air pollution deeply.

Query Complexity of Least Absolute Deviation Regression via Robust Uniform Convergence

Consider a regression problem where the learner is given a large collection of $d$-dimensional data points, but can only query a small subset of the real-valued labels. How many queries are needed to obtain a $1+\epsilon$ relative error approximation of the optimum? While this problem has been extensively studied for least squares regression, little is known for other losses. An important example is least absolute deviation regression ($\ell_1$ regression) which enjoys superior robustness to outliers compared to least squares. We develop a new framework for analyzing importance sampling methods in regression problems, which enables us to show that the query complexity of least absolute deviation regression is $\Theta(d/\epsilon^2)$ up to logarithmic factors. We further extend our techniques to show the first bounds on the query complexity for any $\ell_p$ loss with $p\in(1,2)$. As a key novelty in our analysis, we introduce the notion of robust uniform convergence, which is a new approximation guarantee for the empirical loss. While it is inspired by uniform convergence in statistical learning, our approach additionally incorporates a correction term to avoid unnecessary variance due to outliers. This can be viewed as a new connection between statistical learning theory and variance reduction techniques in stochastic optimization, which should be of independent interest.

Estimating Principal Components under Adversarial Perturbations

Robustness is a key requirement for widespread deployment of machine learning algorithms, and has received much attention in both statistics and computer science. We study a natural model of robustness for high-dimensional statistical estimation problems that we call the adversarial perturbation model. An adversary can perturb every sample arbitrarily up to a specified magnitude $\delta$ measured in some $\ell_q$ norm, say $\ell_\infty$. Our model is motivated by emerging paradigms such as low precision machine learning and adversarial training. We study the classical problem of estimating the top-$r$ principal subspace of the Gaussian covariance matrix in high dimensions, under the adversarial perturbation model. We design a computationally efficient algorithm that given corrupted data, recovers an estimate of the top-$r$ principal subspace with error that depends on a robustness parameter $\kappa$ that we identify. This parameter corresponds to the $q \to 2$ operator norm of the projector onto the principal subspace, and generalizes well-studied analytic notions of sparsity. Additionally, in the absence of corruptions, our algorithmic guarantees recover existing bounds for problems such as sparse PCA and its higher rank analogs. We also prove that the above dependence on the parameter $\kappa$ is almost optimal asymptotically, not just in a minimax sense, but remarkably for every instance of the problem. This instance-optimal guarantee shows that the $q \to 2$ operator norm of the subspace essentially characterizes the estimation error under adversarial perturbations.

Adversarially Robust Low Dimensional Representations

Adversarial or test time robustness measures the susceptibility of a machine learning system to small perturbations made to the input at test time. This has attracted much interest on the empirical side, since many existing ML systems perform poorly under imperceptible adversarial perturbations to the test inputs. On the other hand, our theoretical understanding of this phenomenon is limited, and has mostly focused on supervised learning tasks. In this work we study the problem of computing adversarially robust representations of data. We formulate a natural extension of Principal Component Analysis (PCA) where the goal is to find a low dimensional subspace to represent the given data with minimum projection error, and that is in addition robust to small perturbations measured in $\ell_q$ norm (say $q=\infty$). Unlike PCA which is solvable in polynomial time, our formulation is computationally intractable to optimize as it captures the well-studied sparse PCA objective. We show the following algorithmic and statistical results. - Polynomial time algorithms in the worst-case that achieve constant factor approximations to the objective while only violating the robustness constraint by a constant factor. - We prove that our formulation (and algorithms) also enjoy significant statistical benefits in terms of sample complexity over standard PCA on account of a "regularization effect", that is formalized using the well-studied spiked covariance model. - Surprisingly, we show that our algorithmic techniques can also be made robust to corruptions in the training data, in addition to yielding representations that are robust at test time! Here an adversary is allowed to corrupt potentially every data point up to a specified amount in the $\ell_q$ norm. We further apply these techniques for mean estimation and clustering under adversarial corruptions to the training data.

Active Regression via Linear-Sample Sparsification

We consider the problem of active linear regression with $\ell_2$-bounded noise. In this context, the learner receives a set of unlabeled data points, chooses a small subset to receive the labels for, and must give an estimate of the function that performs well on fresh samples. We give an algorithm that is simultaneously optimal in the number of labeled and unlabeled data points, with $O(d)$ labeled samples; previous work required $\Omega(d \log d)$ labeled samples regardless of the number of unlabeled samples. Our results also apply to learning linear functions from noisy queries, again achieving optimal sample complexities. The techniques extend beyond linear functions, giving improved sample complexities for learning the family of $k$-Fourier-sparse signals with continuous frequencies.