Confined Orthogonal Matching Pursuit for Sparse Random Combinatorial Matrices

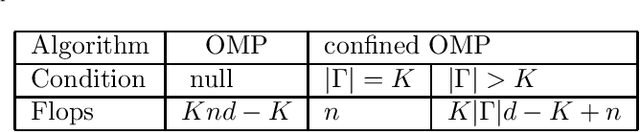
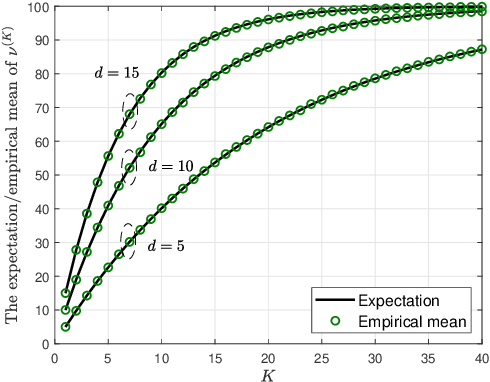
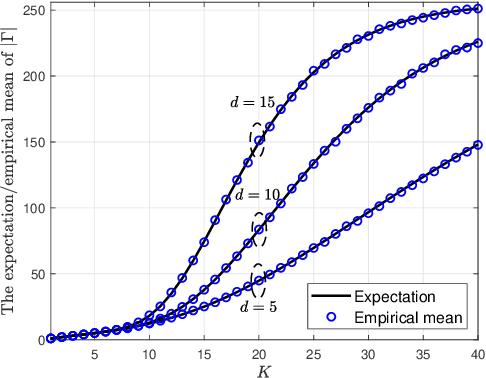
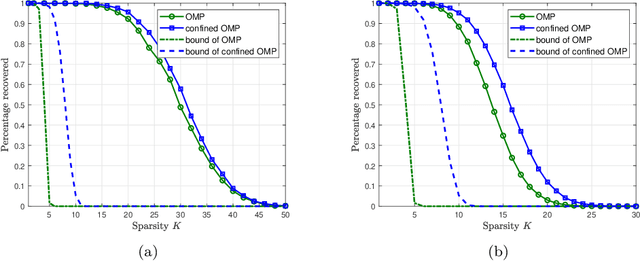
Orthogonal matching pursuit (OMP) is a commonly used greedy algorithm for recovering sparse signals from compressed measurements. In this paper, we introduce a variant of the OMP algorithm to reduce the complexity of reconstructing a class of $K$-sparse signals $\boldsymbol{x} \in \mathbb{R}^{n}$ from measurements $\boldsymbol{y} = \boldsymbol{A}\boldsymbol{x}$, where $\boldsymbol{A} \in \{0,1\}^{m \times n}$ is a sparse random combinatorial matrix with $d~(d \leq m/2)$ ones per column. The proposed algorithm, referred to as the confined OMP algorithm, utilizes the properties of $\boldsymbol{x}$ and $\boldsymbol{A}$ to remove much of the redundancy in the dictionary (also referred to as $\boldsymbol{A}$) and thus fewer column indices of $\boldsymbol{A}$ need to be identified. To this end, we first define a confined set $\Gamma$ with $|\Gamma| \leq n$ and then prove that the support of $\boldsymbol{x}$ is a subset of $\Gamma$ with probability 1 if the distributions of non-zero components of $\boldsymbol{x}$ satisfy a certain condition. During the process of the confined OMP algorithm, the possibly chosen column indices are strictly confined into the confined set $\Gamma$. We further develop lower bounds on the probability of exact recovery of $\boldsymbol{x}$ using OMP algorithm and confined OMP algorithm with $K$ iterations, respectively. The obtained theoretical results of confined OMP algorithm can be used to optimize the column degree $d$ of $\boldsymbol{A}$. Finally, experimental results show that the confined OMP algorithm is more efficient in reconstructing a class of sparse signals compared to the OMP algorithm.

Making GAN-Generated Images Difficult To Spot: A New Attack Against Synthetic Image Detectors

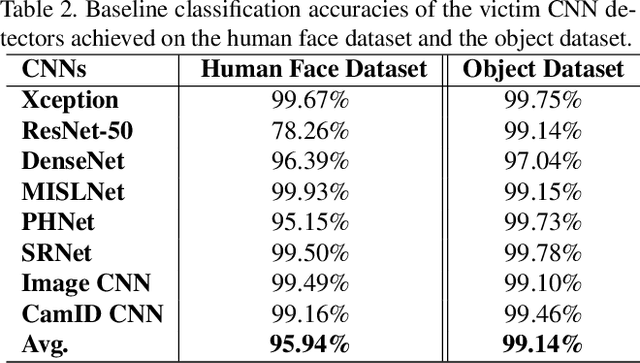
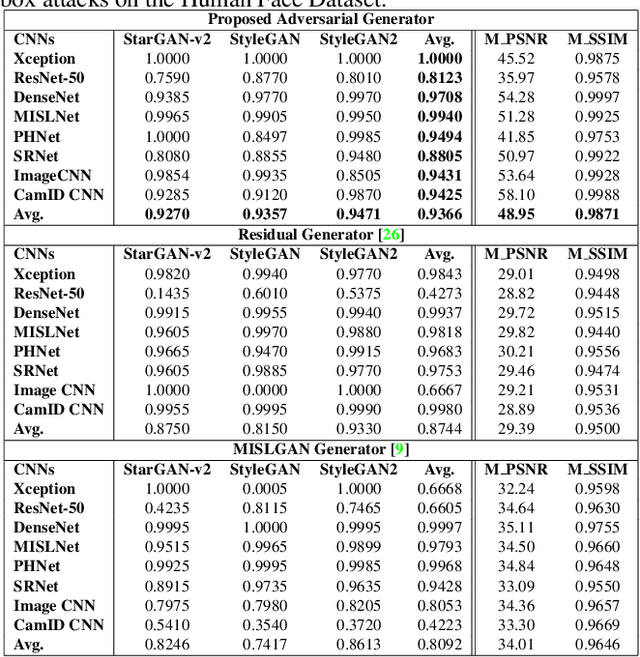
Visually realistic GAN-generated images have recently emerged as an important misinformation threat. Research has shown that these synthetic images contain forensic traces that are readily identifiable by forensic detectors. Unfortunately, these detectors are built upon neural networks, which are vulnerable to recently developed adversarial attacks. In this paper, we propose a new anti-forensic attack capable of fooling GAN-generated image detectors. Our attack uses an adversarially trained generator to synthesize traces that these detectors associate with real images. Furthermore, we propose a technique to train our attack so that it can achieve transferability, i.e. it can fool unknown CNNs that it was not explicitly trained against. We demonstrate the performance of our attack through an extensive set of experiments, where we show that our attack can fool eight state-of-the-art detection CNNs with synthetic images created using seven different GANs.

The Effect of Class Definitions on the Transferability of Adversarial Attacks Against Forensic CNNs

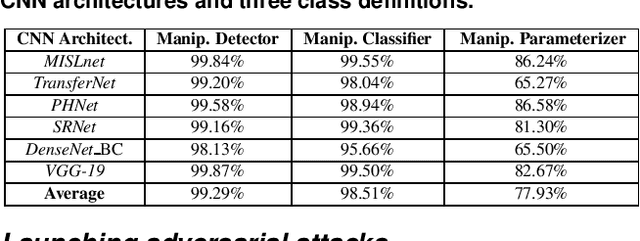
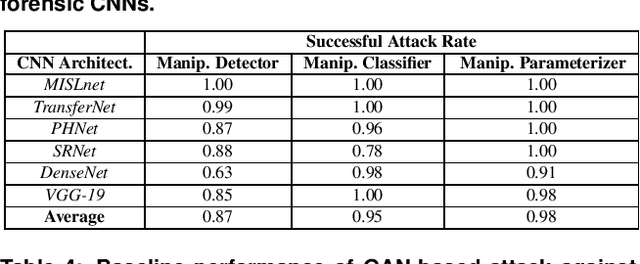
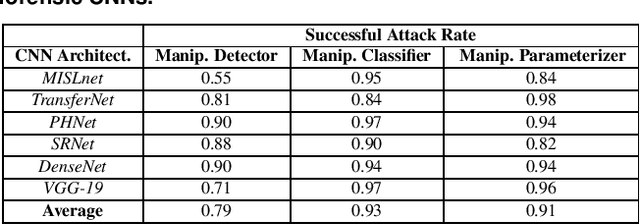
In recent years, convolutional neural networks (CNNs) have been widely used by researchers to perform forensic tasks such as image tampering detection. At the same time, adversarial attacks have been developed that are capable of fooling CNN-based classifiers. Understanding the transferability of adversarial attacks, i.e. an attacks ability to attack a different CNN than the one it was trained against, has important implications for designing CNNs that are resistant to attacks. While attacks on object recognition CNNs are believed to be transferrable, recent work by Barni et al. has shown that attacks on forensic CNNs have difficulty transferring to other CNN architectures or CNNs trained using different datasets. In this paper, we demonstrate that adversarial attacks on forensic CNNs are even less transferrable than previously thought even between virtually identical CNN architectures! We show that several common adversarial attacks against CNNs trained to identify image manipulation fail to transfer to CNNs whose only difference is in the class definitions (i.e. the same CNN architectures trained using the same data). We note that all formulations of class definitions contain the unaltered class. This has important implications for the future design of forensic CNNs that are robust to adversarial and anti-forensic attacks.

Defenses Against Multi-Sticker Physical Domain Attacks on Classifiers

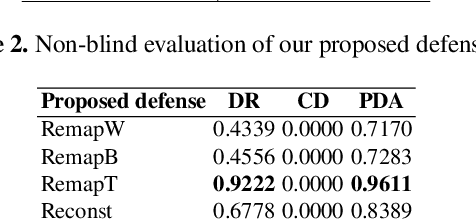
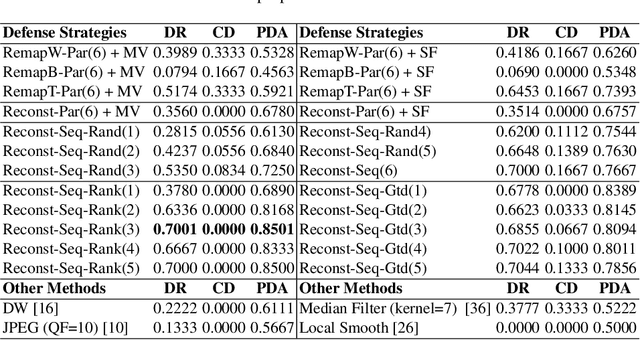
Recently, physical domain adversarial attacks have drawn significant attention from the machine learning community. One important attack proposed by Eykholt et al. can fool a classifier by placing black and white stickers on an object such as a road sign. While this attack may pose a significant threat to visual classifiers, there are currently no defenses designed to protect against this attack. In this paper, we propose new defenses that can protect against multi-sticker attacks. We present defensive strategies capable of operating when the defender has full, partial, and no prior information about the attack. By conducting extensive experiments, we show that our proposed defenses can outperform existing defenses against physical attacks when presented with a multi-sticker attack.

A Transferable Anti-Forensic Attack on Forensic CNNs Using A Generative Adversarial Network

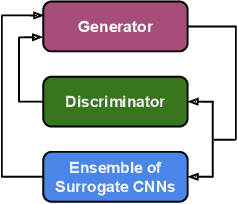
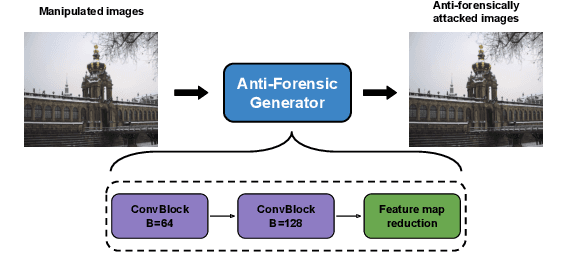
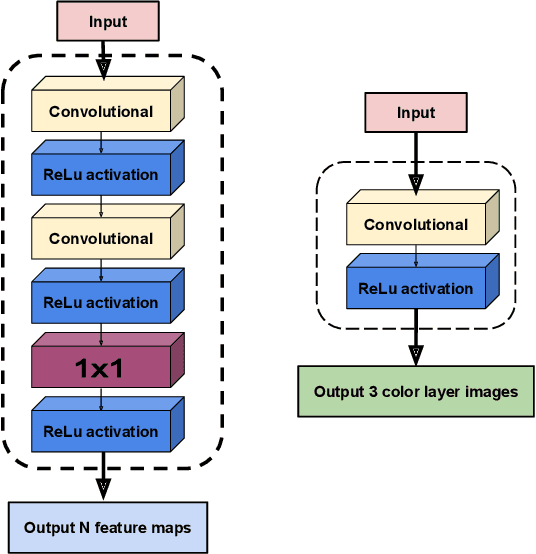
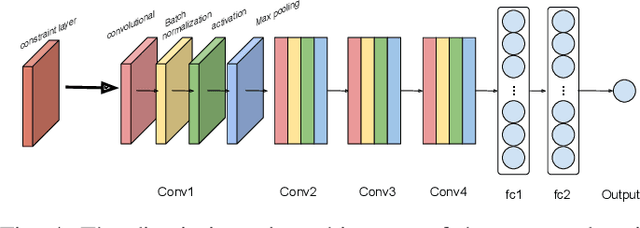
With the development of deep learning, convolutional neural networks (CNNs) have become widely used in multimedia forensics for tasks such as detecting and identifying image forgeries. Meanwhile, anti-forensic attacks have been developed to fool these CNN-based forensic algorithms. Previous anti-forensic attacks often were designed to remove forgery traces left by a single manipulation operation as opposed to a set of manipulations. Additionally, recent research has shown that existing anti-forensic attacks against forensic CNNs have poor transferability, i.e. they are unable to fool other forensic CNNs that were not explicitly used during training. In this paper, we propose a new anti-forensic attack framework designed to remove forensic traces left by a variety of manipulation operations. This attack is transferable, i.e. it can be used to attack forensic CNNs are unknown to the attacker, and it introduces only minimal distortions that are imperceptible to human eyes. Our proposed attack utilizes a generative adversarial network (GAN) to build a generator that can attack color images of any size. We achieve attack transferability through the use of a new training strategy and loss function. We conduct extensive experiment to demonstrate that our attack can fool many state-of-art forensic CNNs with varying levels of knowledge available to the attacker.