Confined Orthogonal Matching Pursuit for Sparse Random Combinatorial Matrices
Paper and Code
Jan 02, 2025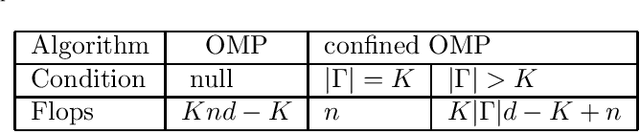
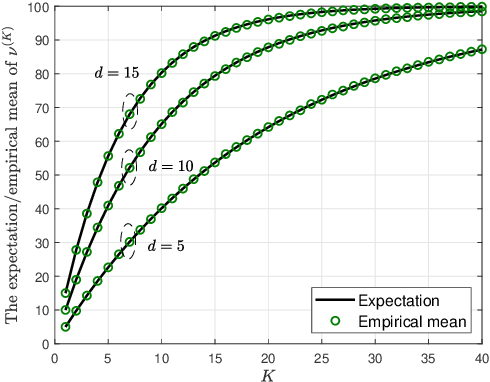
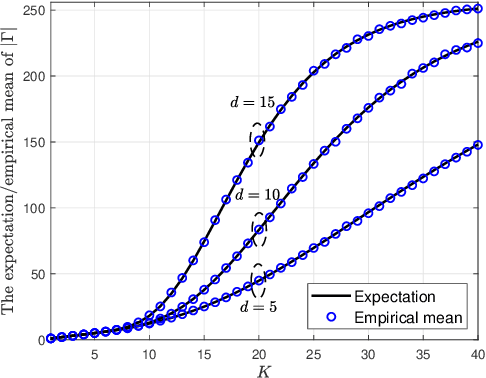
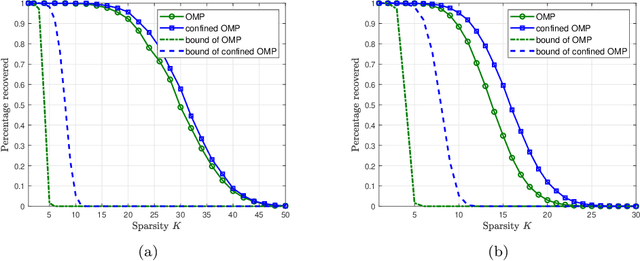
Orthogonal matching pursuit (OMP) is a commonly used greedy algorithm for recovering sparse signals from compressed measurements. In this paper, we introduce a variant of the OMP algorithm to reduce the complexity of reconstructing a class of $K$-sparse signals $\boldsymbol{x} \in \mathbb{R}^{n}$ from measurements $\boldsymbol{y} = \boldsymbol{A}\boldsymbol{x}$, where $\boldsymbol{A} \in \{0,1\}^{m \times n}$ is a sparse random combinatorial matrix with $d~(d \leq m/2)$ ones per column. The proposed algorithm, referred to as the confined OMP algorithm, utilizes the properties of $\boldsymbol{x}$ and $\boldsymbol{A}$ to remove much of the redundancy in the dictionary (also referred to as $\boldsymbol{A}$) and thus fewer column indices of $\boldsymbol{A}$ need to be identified. To this end, we first define a confined set $\Gamma$ with $|\Gamma| \leq n$ and then prove that the support of $\boldsymbol{x}$ is a subset of $\Gamma$ with probability 1 if the distributions of non-zero components of $\boldsymbol{x}$ satisfy a certain condition. During the process of the confined OMP algorithm, the possibly chosen column indices are strictly confined into the confined set $\Gamma$. We further develop lower bounds on the probability of exact recovery of $\boldsymbol{x}$ using OMP algorithm and confined OMP algorithm with $K$ iterations, respectively. The obtained theoretical results of confined OMP algorithm can be used to optimize the column degree $d$ of $\boldsymbol{A}$. Finally, experimental results show that the confined OMP algorithm is more efficient in reconstructing a class of sparse signals compared to the OMP algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge