Multi-hop Upstream Preemptive Traffic Signal Control with Deep Reinforcement Learning

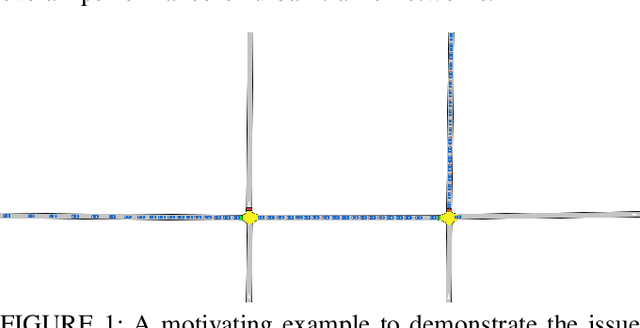
Traffic signal control is crucial for managing congestion in urban networks. Existing myopic pressure-based control methods focus only on immediate upstream links, leading to suboptimal green time allocation and increased network delays. Effective signal control, however, inherently requires a broader spatial scope, as traffic conditions further upstream can significantly impact traffic at the current location. This paper introduces a novel concept based on the Markov chain theory, namely multi-hop upstream pressure, that generalizes the conventional pressure to account for traffic conditions beyond the immediate upstream links. This farsighted and compact metric informs the deep reinforcement learning agent to preemptively clear the present queues, guiding the agent to optimize signal timings with a broader spatial awareness. Simulations on synthetic and realistic (Toronto) scenarios demonstrate controllers utilizing multi-hop upstream pressure significantly reduce overall network delay by prioritizing traffic movements based on a broader understanding of upstream congestion.

Generalized Multi-hop Traffic Pressure for Heterogeneous Traffic Perimeter Control

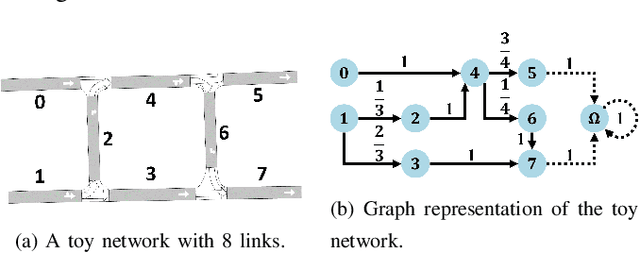
Perimeter control prevents loss of traffic network capacity due to congestion in urban areas. Homogeneous perimeter control allows all access points to a protected region to have the same maximal permitted inflow. However, homogeneous perimeter control performs poorly when the congestion in the protected region is heterogeneous (e.g., imbalanced demand) since the homogeneous perimeter control does not consider location-specific traffic conditions around the perimeter. When the protected region has spatially heterogeneous congestion, it can often make sense to modulate the perimeter inflow rate to be higher near low-density regions and vice versa for high-density regions. To assist with this modulation, we can leverage the concept of 1-hop traffic pressure to measure intersection-level traffic congestion. However, as we show, 1-hop pressure turns out to be too spatially myopic for perimeter control and hence we formulate multi-hop generalizations of pressure that look ``deeper'' inside the perimeter beyond the entry intersection. In addition, we formulate a simple heterogeneous perimeter control methodology that can leverage this novel multi-hop pressure to redistribute the total permitted inflow provided by the homogeneous perimeter controller. Experimental results show that our heterogeneous perimeter control policies leveraging multi-hop pressure significantly outperform homogeneous perimeter control in scenarios where the origin-destination flows are highly imbalanced with high spatial heterogeneity.

Revisiting Random Forests in a Comparative Evaluation of Graph Convolutional Neural Network Variants for Traffic Prediction

Traffic prediction is a spatiotemporal predictive task that plays an essential role in intelligent transportation systems. Today, graph convolutional neural networks (GCNNs) have become the prevailing models in the traffic prediction literature since they excel at extracting spatial correlations. In this work, we classify the components of successful GCNN prediction models and analyze the effects of matrix factorization, attention mechanism, and weight sharing on their performance. Furthermore, we compare these variations against random forests, a traditional regression method that predates GCNNs by over 15 years. We evaluated these methods using simulated data of two regions in Toronto as well as real-world sensor data from selected California highways. We found that incorporating matrix factorization, attention, and location-specific model weights either individually or collectively into GCNNs can result in a better overall performance. Moreover, although random forest regression is a less compact model, it matches or exceeds the performance of all variations of GCNNs in our experiments. This suggests that the current graph convolutional methods may not be the best approach to traffic prediction and there is still room for improvement. Finally, our findings also suggest that for future research on GCNN for traffic prediction to be credible, researchers must include performance comparison to random forests.

Perimeter Control Using Deep Reinforcement Learning: A Model-free Approach towards Homogeneous Flow Rate Optimization

Perimeter control maintains high traffic efficiency within protected regions by controlling transfer flows among regions to ensure that their traffic densities are below critical values. Existing approaches can be categorized as either model-based or model-free, depending on whether they rely on network transmission models (NTMs) and macroscopic fundamental diagrams (MFDs). Although model-based approaches are more data efficient and have performance guarantees, they are inherently prone to model bias and inaccuracy. For example, NTMs often become imprecise for a large number of protected regions, and MFDs can exhibit scatter and hysteresis that are not captured in existing model-based works. Moreover, no existing studies have employed reinforcement learning for homogeneous flow rate optimization in microscopic simulation, where spatial characteristics, vehicle-level information, and metering realizations -- often overlooked in macroscopic simulations -- are taken into account. To circumvent issues of model-based approaches and macroscopic simulation, we propose a model-free deep reinforcement learning approach that optimizes the flow rate homogeneously at the perimeter at the microscopic level. Results demonstrate that our model-free reinforcement learning approach without any knowledge of NTMs or MFDs can compete and match the performance of a model-based approach, and exhibits enhanced generalizability and scalability.

FameSVD: Fast and Memory-efficient Singular Value Decomposition

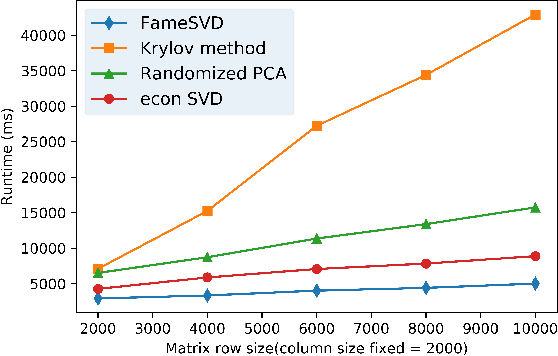
We propose a novel algorithm to perform the Singular Value Decomposition (SVD) by leveraging the internal property of SVD. Due to the derivation being explored deterministically rather than stochastically, the convergence is guaranteed. Complexity analysis is also conducted. Our proposed SVD method outperforms classic algorithms with significant margin both in runtime and memory usage. Furthermore, we discuss the relationship between SVD and Principal Component Analysis (PCA). For those SVD or PCA algorithms that do not acquire all eigenvalues or cannot get them precisely, we utilize the matrix analysis knowledge to get the sum of all eigenvalues in order that cumulative explained variance criterion could be used in not-all-eigenvalues-are-known cases.