FameSVD: Fast and Memory-efficient Singular Value Decomposition

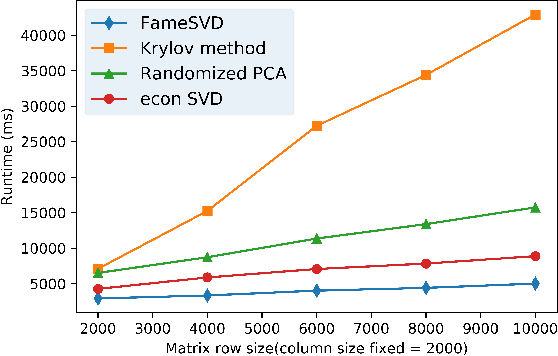
We propose a novel algorithm to perform the Singular Value Decomposition (SVD) by leveraging the internal property of SVD. Due to the derivation being explored deterministically rather than stochastically, the convergence is guaranteed. Complexity analysis is also conducted. Our proposed SVD method outperforms classic algorithms with significant margin both in runtime and memory usage. Furthermore, we discuss the relationship between SVD and Principal Component Analysis (PCA). For those SVD or PCA algorithms that do not acquire all eigenvalues or cannot get them precisely, we utilize the matrix analysis knowledge to get the sum of all eigenvalues in order that cumulative explained variance criterion could be used in not-all-eigenvalues-are-known cases.