Emoji Driven Crypto Assets Market Reactions

In the burgeoning realm of cryptocurrency, social media platforms like Twitter have become pivotal in influencing market trends and investor sentiments. In our study, we leverage GPT-4 and a fine-tuned transformer-based BERT model for a multimodal sentiment analysis, focusing on the impact of emoji sentiment on cryptocurrency markets. By translating emojis into quantifiable sentiment data, we correlate these insights with key market indicators like BTC Price and the VCRIX index. This approach may be fed into the development of trading strategies aimed at utilizing social media elements to identify and forecast market trends. Crucially, our findings suggest that strategies based on emoji sentiment can facilitate the avoidance of significant market downturns and contribute to the stabilization of returns. This research underscores the practical benefits of integrating advanced AI-driven analyses into financial strategies, offering a nuanced perspective on the interplay between digital communication and market dynamics in an academic context.

Forecasting Cryptocurrency Prices Using Deep Learning: Integrating Financial, Blockchain, and Text Data

This paper explores the application of Machine Learning (ML) and Natural Language Processing (NLP) techniques in cryptocurrency price forecasting, specifically Bitcoin (BTC) and Ethereum (ETH). Focusing on news and social media data, primarily from Twitter and Reddit, we analyse the influence of public sentiment on cryptocurrency valuations using advanced deep learning NLP methods. Alongside conventional price regression, we treat cryptocurrency price forecasting as a classification problem. This includes both the prediction of price movements (up or down) and the identification of local extrema. We compare the performance of various ML models, both with and without NLP data integration. Our findings reveal that incorporating NLP data significantly enhances the forecasting performance of our models. We discover that pre-trained models, such as Twitter-RoBERTa and BART MNLI, are highly effective in capturing market sentiment, and that fine-tuning Large Language Models (LLMs) also yields substantial forecasting improvements. Notably, the BART MNLI zero-shot classification model shows considerable proficiency in extracting bullish and bearish signals from textual data. All of our models consistently generate profit across different validation scenarios, with no observed decline in profits or reduction in the impact of NLP data over time. The study highlights the potential of text analysis in improving financial forecasts and demonstrates the effectiveness of various NLP techniques in capturing nuanced market sentiment.

Robustifying Markowitz

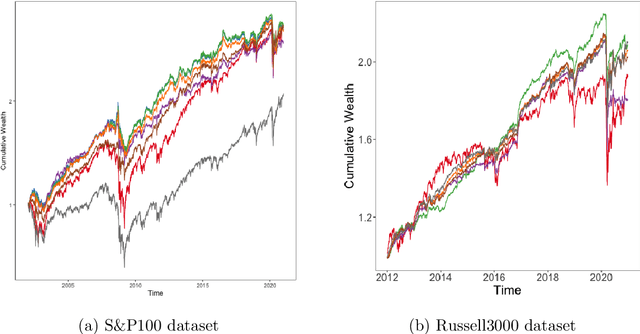
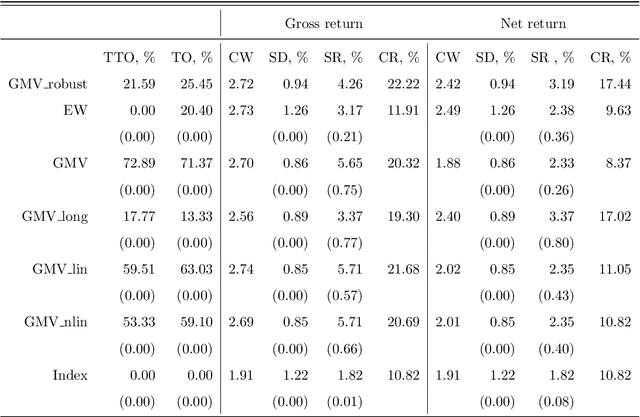
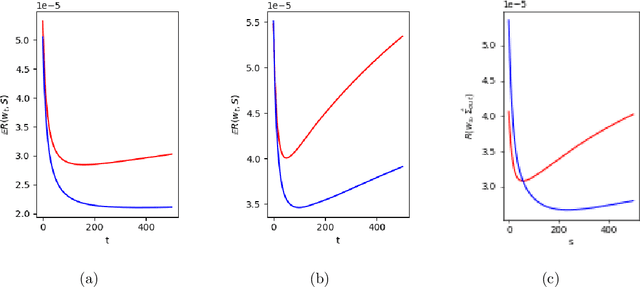
Markowitz mean-variance portfolios with sample mean and covariance as input parameters feature numerous issues in practice. They perform poorly out of sample due to estimation error, they experience extreme weights together with high sensitivity to change in input parameters. The heavy-tail characteristics of financial time series are in fact the cause for these erratic fluctuations of weights that consequently create substantial transaction costs. In robustifying the weights we present a toolbox for stabilizing costs and weights for global minimum Markowitz portfolios. Utilizing a projected gradient descent (PGD) technique, we avoid the estimation and inversion of the covariance operator as a whole and concentrate on robust estimation of the gradient descent increment. Using modern tools of robust statistics we construct a computationally efficient estimator with almost Gaussian properties based on median-of-means uniformly over weights. This robustified Markowitz approach is confirmed by empirical studies on equity markets. We demonstrate that robustified portfolios reach the lowest turnover compared to shrinkage-based and constrained portfolios while preserving or slightly improving out-of-sample performance.

Shapley Curves: A Smoothing Perspective

Originating from cooperative game theory, Shapley values have become one of the most widely used measures for variable importance in applied Machine Learning. However, the statistical understanding of Shapley values is still limited. In this paper, we take a nonparametric (or smoothing) perspective by introducing Shapley curves as a local measure of variable importance. We propose two estimation strategies and derive the consistency and asymptotic normality both under independence and dependence among the features. This allows us to construct confidence intervals and conduct inference on the estimated Shapley curves. The asymptotic results are validated in extensive experiments. In an empirical application, we analyze which attributes drive the prices of vehicles.

A Data-driven Case-based Reasoning in Bankruptcy Prediction

There has been intensive research regarding machine learning models for predicting bankruptcy in recent years. However, the lack of interpretability limits their growth and practical implementation. This study proposes a data-driven explainable case-based reasoning (CBR) system for bankruptcy prediction. Empirical results from a comparative study show that the proposed approach performs superior to existing, alternative CBR systems and is competitive with state-of-the-art machine learning models. We also demonstrate that the asymmetrical feature similarity comparison mechanism in the proposed CBR system can effectively capture the asymmetrically distributed nature of financial attributes, such as a few companies controlling more cash than the majority, hence improving both the accuracy and explainability of predictions. In addition, we delicately examine the explainability of the CBR system in the decision-making process of bankruptcy prediction. While much research suggests a trade-off between improving prediction accuracy and explainability, our findings show a prospective research avenue in which an explainable model that thoroughly incorporates data attributes by design can reconcile the dilemma.

Does non-linear factorization of financial returns help build better and stabler portfolios?

A portfolio allocation method based on linear and non-linear latent constrained conditional factors is presented. The factor loadings are constrained to always be positive in order to obtain long-only portfolios, which is not guaranteed by classical factor analysis or PCA. In addition, the factors are to be uncorrelated among clusters in order to build long-only portfolios. Our approach is based on modern machine learning tools: convex Non-negative Matrix Factorization (NMF) and autoencoder neural networks, designed in a specific manner to enforce the learning of useful hidden data structure such as correlation between the assets' returns. Our technique finds lowly correlated linear and non-linear conditional latent factors which are used to build outperforming global portfolios consisting of cryptocurrencies and traditional assets, similar to hierarchical clustering method. We study the dynamics of the derived non-linear factors in order to forecast tail losses of the portfolios and thus build more stable ones.

K-expectiles clustering

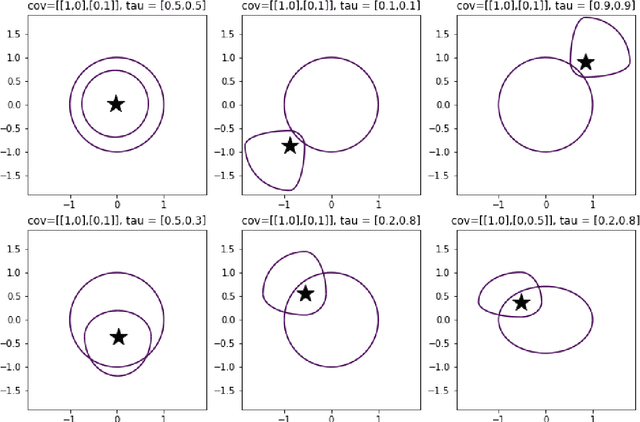
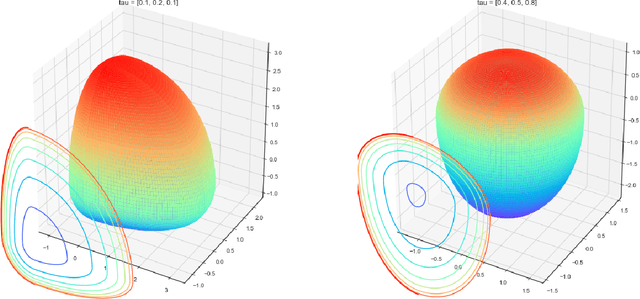
$K$-means clustering is one of the most widely-used partitioning algorithm in cluster analysis due to its simplicity and computational efficiency. However, $K$-means does not provide an appropriate clustering result when applying to data with non-spherically shaped clusters. We propose a novel partitioning clustering algorithm based on expectiles. The cluster centers are defined as multivariate expectiles and clusters are searched via a greedy algorithm by minimizing the within cluster '$\tau$ -variance'. We suggest two schemes: fixed $\tau$ clustering, and adaptive $\tau$ clustering. Validated by simulation results, this method beats both $K$-means and spectral clustering on data with asymmetric shaped clusters, or clusters with a complicated structure, including asymmetric normal, beta, skewed $t$ and $F$ distributed clusters. Applications of adaptive $\tau$ clustering on crypto-currency (CC) market data are provided. One finds that the expectiles clusters of CC markets show the phenomena of an institutional investors dominated market. The second application is on image segmentation. compared to other center based clustering methods, the adaptive $\tau$ cluster centers of pixel data can better capture and describe the features of an image. The fixed $\tau$ clustering brings more flexibility on segmentation with a decent accuracy.

Surrogate Models for Optimization of Dynamical Systems

Driven by increased complexity of dynamical systems, the solution of system of differential equations through numerical simulation in optimization problems has become computationally expensive. This paper provides a smart data driven mechanism to construct low dimensional surrogate models. These surrogate models reduce the computational time for solution of the complex optimization problems by using training instances derived from the evaluations of the true objective functions. The surrogate models are constructed using combination of proper orthogonal decomposition and radial basis functions and provides system responses by simple matrix multiplication. Using relative maximum absolute error as the measure of accuracy of approximation, it is shown surrogate models with latin hypercube sampling and spline radial basis functions dominate variable order methods in computational time of optimization, while preserving the accuracy. These surrogate models also show robustness in presence of model non-linearities. Therefore, these computational efficient predictive surrogate models are applicable in various fields, specifically to solve inverse problems and optimal control problems, some examples of which are demonstrated in this paper.

Group Average Treatment Effects for Observational Studies

The paper proposes an estimator to make inference of heterogeneous treatment effects sorted by impact groups (GATES) for non-randomised experiments. Observational studies are standard in policy evaluation from labour markets, educational surveys and other empirical studies. To control for a potential selection-bias we implement a doubly-robust estimator in the first stage. Keeping the flexibility, we can use any machine learning method to learn the conditional mean functions as well as the propensity score. We also use machine learning methods to learn a function for the conditional average treatment effect. The group average treatment effect, is then estimated via a parametric linear model to provide p-values and confidence intervals. To control for confounding in the linear model we use Neyman-orthogonal moments to partial out the effect that covariates have on both, the treatment assignment and the outcome. The result is a best linear predictor for effect heterogeneity based on impact groups. We introduce inclusion-probability weighting as a form of cross-splitting and averaging for each observation to avoid biases through sample splitting. The advantage of the proposed method is a robust linear estimation of heterogeneous group treatment effects in observational studies.