K-expectiles clustering
Paper and Code
Mar 16, 2021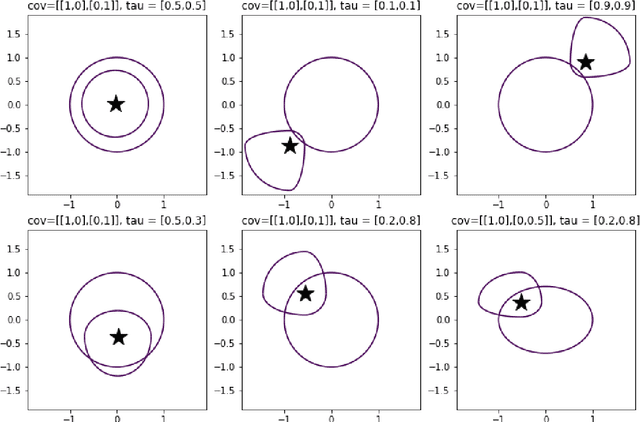
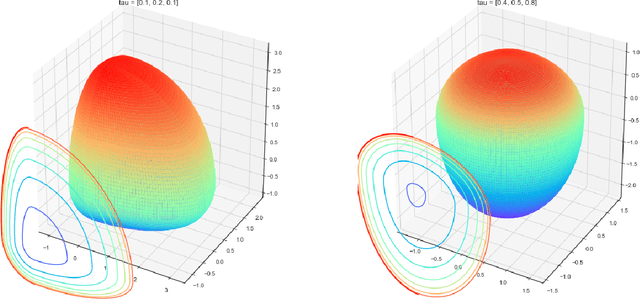


$K$-means clustering is one of the most widely-used partitioning algorithm in cluster analysis due to its simplicity and computational efficiency. However, $K$-means does not provide an appropriate clustering result when applying to data with non-spherically shaped clusters. We propose a novel partitioning clustering algorithm based on expectiles. The cluster centers are defined as multivariate expectiles and clusters are searched via a greedy algorithm by minimizing the within cluster '$\tau$ -variance'. We suggest two schemes: fixed $\tau$ clustering, and adaptive $\tau$ clustering. Validated by simulation results, this method beats both $K$-means and spectral clustering on data with asymmetric shaped clusters, or clusters with a complicated structure, including asymmetric normal, beta, skewed $t$ and $F$ distributed clusters. Applications of adaptive $\tau$ clustering on crypto-currency (CC) market data are provided. One finds that the expectiles clusters of CC markets show the phenomena of an institutional investors dominated market. The second application is on image segmentation. compared to other center based clustering methods, the adaptive $\tau$ cluster centers of pixel data can better capture and describe the features of an image. The fixed $\tau$ clustering brings more flexibility on segmentation with a decent accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge