Bingling Wang
K-expectiles clustering
Mar 16, 2021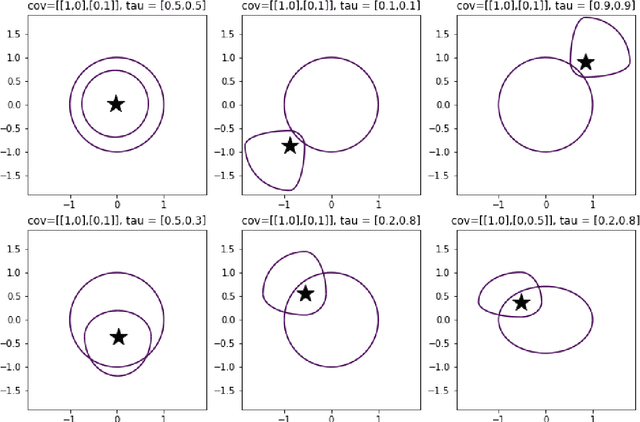
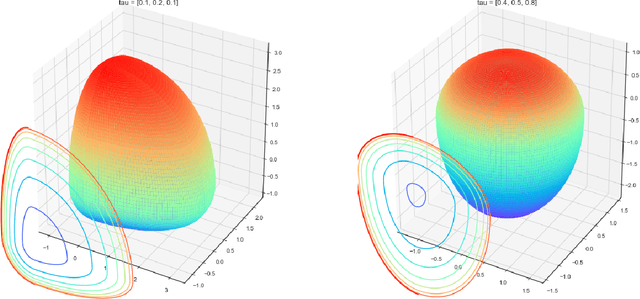


Abstract:$K$-means clustering is one of the most widely-used partitioning algorithm in cluster analysis due to its simplicity and computational efficiency. However, $K$-means does not provide an appropriate clustering result when applying to data with non-spherically shaped clusters. We propose a novel partitioning clustering algorithm based on expectiles. The cluster centers are defined as multivariate expectiles and clusters are searched via a greedy algorithm by minimizing the within cluster '$\tau$ -variance'. We suggest two schemes: fixed $\tau$ clustering, and adaptive $\tau$ clustering. Validated by simulation results, this method beats both $K$-means and spectral clustering on data with asymmetric shaped clusters, or clusters with a complicated structure, including asymmetric normal, beta, skewed $t$ and $F$ distributed clusters. Applications of adaptive $\tau$ clustering on crypto-currency (CC) market data are provided. One finds that the expectiles clusters of CC markets show the phenomena of an institutional investors dominated market. The second application is on image segmentation. compared to other center based clustering methods, the adaptive $\tau$ cluster centers of pixel data can better capture and describe the features of an image. The fixed $\tau$ clustering brings more flexibility on segmentation with a decent accuracy.
Causal network learning with non-invertible functional relationships
Apr 20, 2020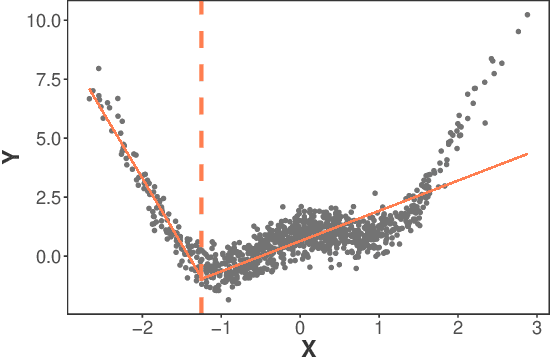

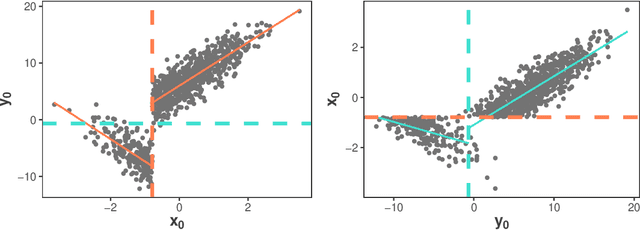
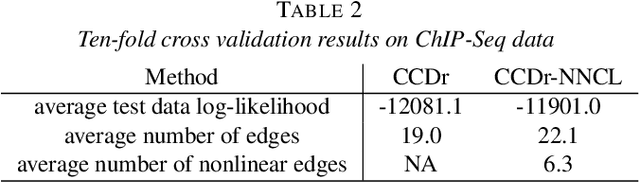
Abstract:Discovery of causal relationships from observational data is an important problem in many areas. Several recent results have established the identifiability of causal DAGs with non-Gaussian and/or nonlinear structural equation models (SEMs). In this paper, we focus on nonlinear SEMs defined by non-invertible functions, which exist in many data domains, and propose a novel test for non-invertible bivariate causal models. We further develop a method to incorporate this test in structure learning of DAGs that contain both linear and nonlinear causal relations. By extensive numerical comparisons, we show that our algorithms outperform existing DAG learning methods in identifying causal graphical structures. We illustrate the practical application of our method in learning causal networks for combinatorial binding of transcription factors from ChIP-Seq data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge