Social Choice for AI Alignment: Dealing with Diverse Human Feedback

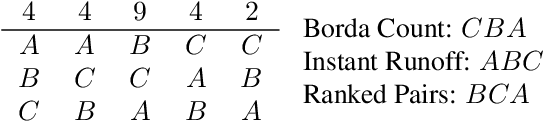
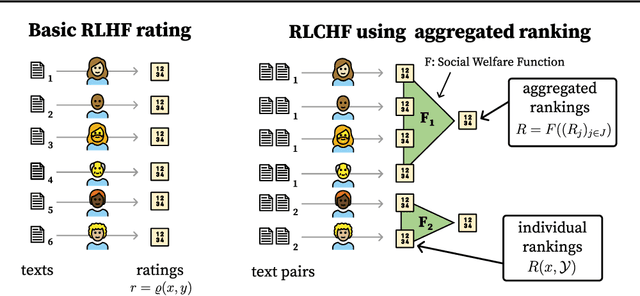
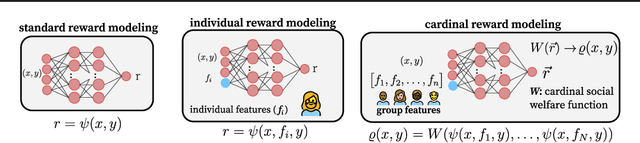
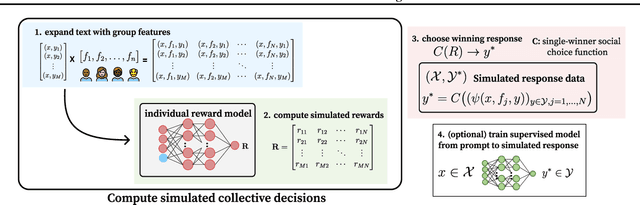
Foundation models such as GPT-4 are fine-tuned to avoid unsafe or otherwise problematic behavior, so that, for example, they refuse to comply with requests for help with committing crimes or with producing racist text. One approach to fine-tuning, called reinforcement learning from human feedback, learns from humans' expressed preferences over multiple outputs. Another approach is constitutional AI, in which the input from humans is a list of high-level principles. But how do we deal with potentially diverging input from humans? How can we aggregate the input into consistent data about ''collective'' preferences or otherwise use it to make collective choices about model behavior? In this paper, we argue that the field of social choice is well positioned to address these questions, and we discuss ways forward for this agenda, drawing on discussions in a recent workshop on Social Choice for AI Ethics and Safety held in Berkeley, CA, USA in December 2023.

Conditional and Modal Reasoning in Large Language Models

The reasoning abilities of large language models (LLMs) are the topic of a growing body of research in artificial intelligence and cognitive science. In this paper, we probe the extent to which a dozen LLMs are able to distinguish logically correct inferences from logically fallacious ones. We focus on inference patterns involving conditionals (e.g., 'If Ann has a queen, then Bob has a jack') and epistemic modals (e.g., 'Ann might have an ace', 'Bob must have a king'). These inference patterns have been of special interest to logicians, philosophers, and linguists, since they plausibly play a central role in human reasoning. Assessing LLMs on these inference patterns is thus highly relevant to the question of how much the reasoning abilities of LLMs match those of humans. Among the LLMs we tested, all but GPT-4 often make basic mistakes with conditionals. Moreover, even GPT-4 displays logically inconsistent judgments across inference patterns involving epistemic modals.

Learning to Manipulate under Limited Information

By classic results in social choice theory, any reasonable preferential voting method sometimes gives individuals an incentive to report an insincere preference. The extent to which different voting methods are more or less resistant to such strategic manipulation has become a key consideration for comparing voting methods. Here we measure resistance to manipulation by whether neural networks of varying sizes can learn to profitably manipulate a given voting method in expectation, given different types of limited information about how other voters will vote. We trained nearly 40,000 neural networks of 26 sizes to manipulate against 8 different voting methods, under 6 types of limited information, in committee-sized elections with 5-21 voters and 3-6 candidates. We find that some voting methods, such as Borda, are highly manipulable by networks with limited information, while others, such as Instant Runoff, are not, despite being quite profitably manipulated by an ideal manipulator with full information.

Preferential Structures for Comparative Probabilistic Reasoning

Qualitative and quantitative approaches to reasoning about uncertainty can lead to different logical systems for formalizing such reasoning, even when the language for expressing uncertainty is the same. In the case of reasoning about relative likelihood, with statements of the form $\varphi\succsim\psi$ expressing that $\varphi$ is at least as likely as $\psi$, a standard qualitative approach using preordered preferential structures yields a dramatically different logical system than a quantitative approach using probability measures. In fact, the standard preferential approach validates principles of reasoning that are incorrect from a probabilistic point of view. However, in this paper we show that a natural modification of the preferential approach yields exactly the same logical system as a probabilistic approach--not using single probability measures, but rather sets of probability measures. Thus, the same preferential structures used in the study of non-monotonic logics and belief revision may be used in the study of comparative probabilistic reasoning based on imprecise probabilities.