Unifying Dual-Space Embedding for Entity Alignment via Contrastive Learning

Entity alignment aims to match identical entities across different knowledge graphs (KGs). Graph neural network-based entity alignment methods have achieved promising results in Euclidean space. However, KGs often contain complex structures, including both local and hierarchical ones, which make it challenging to efficiently represent them within a single space. In this paper, we proposed a novel method UniEA, which unifies dual-space embedding to preserve the intrinsic structure of KGs. Specifically, we learn graph structure embedding in both Euclidean and hyperbolic spaces simultaneously to maximize the consistency between the embedding in both spaces. Moreover, we employ contrastive learning to mitigate the misalignment issues caused by similar entities, where embedding of similar neighboring entities within the KG become too close in distance. Extensive experiments on benchmark datasets demonstrate that our method achieves state-of-the-art performance in structure-based EA. Our code is available at https://github.com/wonderCS1213/UniEA.

Distance-Adaptive Quaternion Knowledge Graph Embedding with Bidirectional Rotation

Quaternion contains one real part and three imaginary parts, which provided a more expressive hypercomplex space for learning knowledge graph. Existing quaternion embedding models measure the plausibility of a triplet either through semantic matching or geometric distance scoring functions. However, it appears that semantic matching diminishes the separability of entities, while the distance scoring function weakens the semantics of entities. To address this issue, we propose a novel quaternion knowledge graph embedding model. Our model combines semantic matching with entity's geometric distance to better measure the plausibility of triplets. Specifically, in the quaternion space, we perform a right rotation on head entity and a reverse rotation on tail entity to learn rich semantic features. Then, we utilize distance adaptive translations to learn geometric distance between entities. Furthermore, we provide mathematical proofs to demonstrate our model can handle complex logical relationships. Extensive experimental results and analyses show our model significantly outperforms previous models on well-known knowledge graph completion benchmark datasets. Our code is available at https://github.com/llqy123/DaBR.

Fully Hyperbolic Rotation for Knowledge Graph Embedding

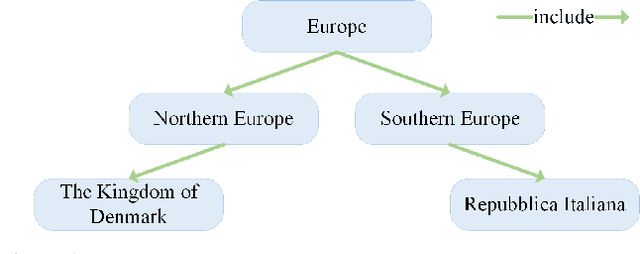
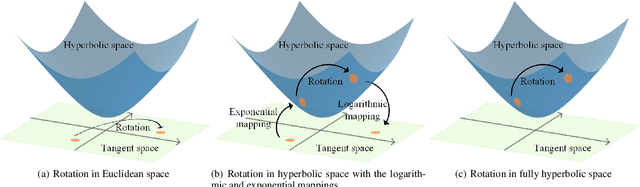
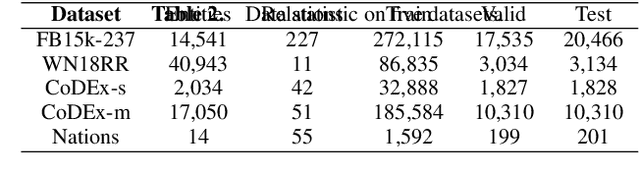
Hyperbolic rotation is commonly used to effectively model knowledge graphs and their inherent hierarchies. However, existing hyperbolic rotation models rely on logarithmic and exponential mappings for feature transformation. These models only project data features into hyperbolic space for rotation, limiting their ability to fully exploit the hyperbolic space. To address this problem, we propose a novel fully hyperbolic model designed for knowledge graph embedding. Instead of feature mappings, we define the model directly in hyperbolic space with the Lorentz model. Our model considers each relation in knowledge graphs as a Lorentz rotation from the head entity to the tail entity. We adopt the Lorentzian version distance as the scoring function for measuring the plausibility of triplets. Extensive results on standard knowledge graph completion benchmarks demonstrated that our model achieves competitive results with fewer parameters. In addition, our model get the state-of-the-art performance on datasets of CoDEx-s and CoDEx-m, which are more diverse and challenging than before. Our code is available at https://github.com/llqy123/FHRE.

L$^2$GC: Lorentzian Linear Graph Convolutional Networks For Node Classification

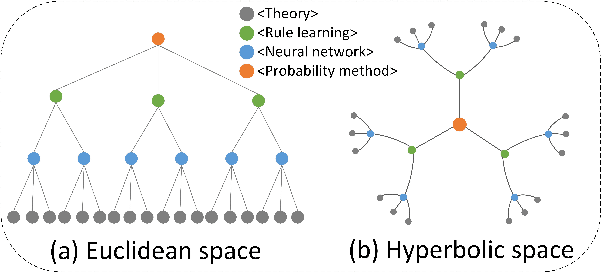
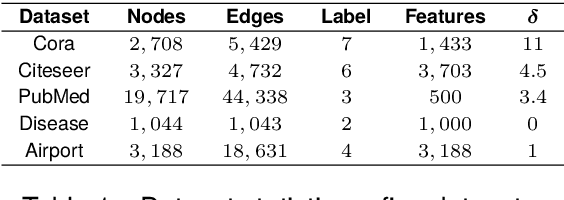
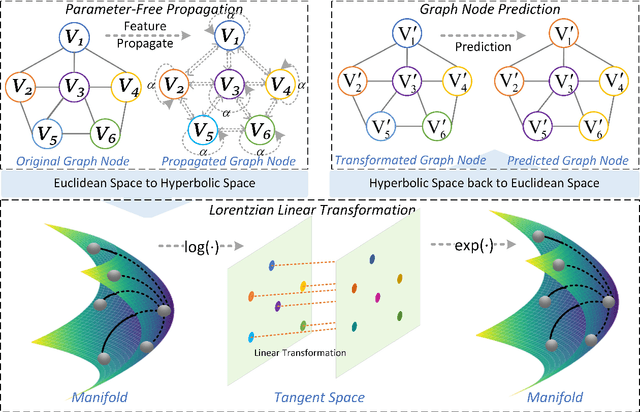
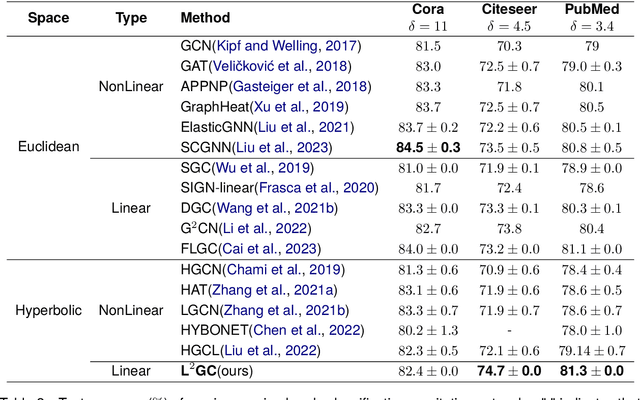
Linear Graph Convolutional Networks (GCNs) are used to classify the node in the graph data. However, we note that most existing linear GCN models perform neural network operations in Euclidean space, which do not explicitly capture the tree-like hierarchical structure exhibited in real-world datasets that modeled as graphs. In this paper, we attempt to introduce hyperbolic space into linear GCN and propose a novel framework for Lorentzian linear GCN. Specifically, we map the learned features of graph nodes into hyperbolic space, and then perform a Lorentzian linear feature transformation to capture the underlying tree-like structure of data. Experimental results on standard citation networks datasets with semi-supervised learning show that our approach yields new state-of-the-art results of accuracy 74.7$\%$ on Citeseer and 81.3$\%$ on PubMed datasets. Furthermore, we observe that our approach can be trained up to two orders of magnitude faster than other nonlinear GCN models on PubMed dataset. Our code is publicly available at https://github.com/llqy123/LLGC-master.

Modelling the Point Spread Function of Wide Field Small Aperture Telescopes With Deep Neural Networks -- Applications in Point Spread Function Estimation

The point spread function (PSF) reflects states of a telescope and plays an important role in development of smart data processing methods. However, for wide field small aperture telescopes (WFSATs), estimating PSF in any position of the whole field of view (FoV) is hard, because aberrations induced by the optical system are quite complex and the signal to noise ratio of star images is often too low for PSF estimation. In this paper, we further develop our deep neural network (DNN) based PSF modelling method and show its applications in PSF estimation. During the telescope alignment and testing stage, our method collects system calibration data through modification of optical elements within engineering tolerances (tilting and decentering). Then we use these data to train a DNN. After training, the DNN can estimate PSF in any field of view from several discretely sampled star images. We use both simulated and experimental data to test performance of our method. The results show that our method could successfully reconstruct PSFs of WFSATs of any states and in any positions of the FoV. Its results are significantly more precise than results obtained by the compared classic method - Inverse Distance Weight (IDW) interpolation. Our method provides foundations for developing of smart data processing methods for WFSATs in the future.

Compressive Shack-Hartmann Wavefront Sensing based on Deep Neural Networks

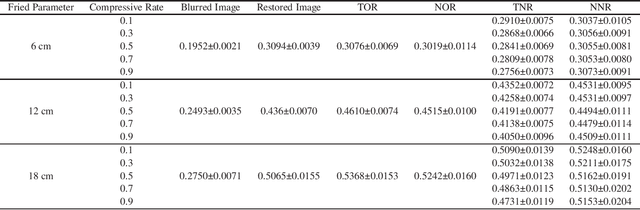
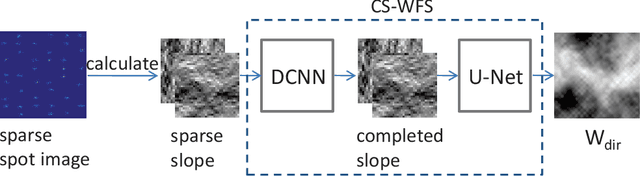
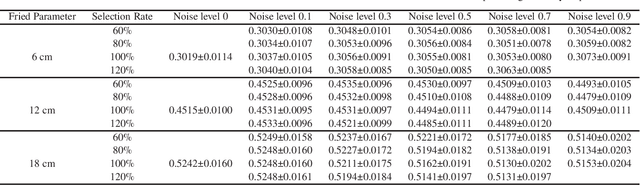
The Shack-Hartmann wavefront sensor is widely used to measure aberrations induced by atmospheric turbulence in adaptive optics systems. However if there exists strong atmospheric turbulence or the brightness of guide stars is low, the accuracy of wavefront measurements will be affected. In this paper, we propose a compressive Shack-Hartmann wavefront sensing method. Instead of reconstructing wavefronts with slope measurements of all sub-apertures, our method reconstructs wavefronts with slope measurements of sub-apertures which have spot images with high signal to noise ratio. Besides, we further propose to use a deep neural network to accelerate wavefront reconstruction speed. During the training stage of the deep neural network, we propose to add a drop-out layer to simulate the compressive sensing process, which could increase development speed of our method. After training, the compressive Shack-Hartmann wavefront sensing method can reconstruct wavefronts in high spatial resolution with slope measurements from only a small amount of sub-apertures. We integrate the straightforward compressive Shack-Hartmann wavefront sensing method with image deconvolution algorithm to develop a high-order image restoration method. We use images restored by the high-order image restoration method to test the performance of our the compressive Shack-Hartmann wavefront sensing method. The results show that our method can improve the accuracy of wavefront measurements and is suitable for real-time applications.