Planning through Workspace Constraint Satisfaction and Optimization

In this work, we present a workspace-based planning framework, which though using redundant workspace key-points to represent robot states, can take advantage of the interpretable geometric information to derive good quality collision-free paths for even complex robots. Using workspace geometries, we first find collision-free piece-wise linear paths for each key point so that at the endpoints of each segment, the distance constraints are satisfied among the key points. Using these piece-wise linear paths as initial conditions, we can perform optimization steps to quickly find paths that satisfy various constraints and piece together all segments to obtain a valid path. We show that these adjusted paths are unlikely to create a collision, and the proposed approach is fast and can produce good quality results.

Planning and Formulations in Pursuit-Evasion: Keep-away Games and Their Strategies

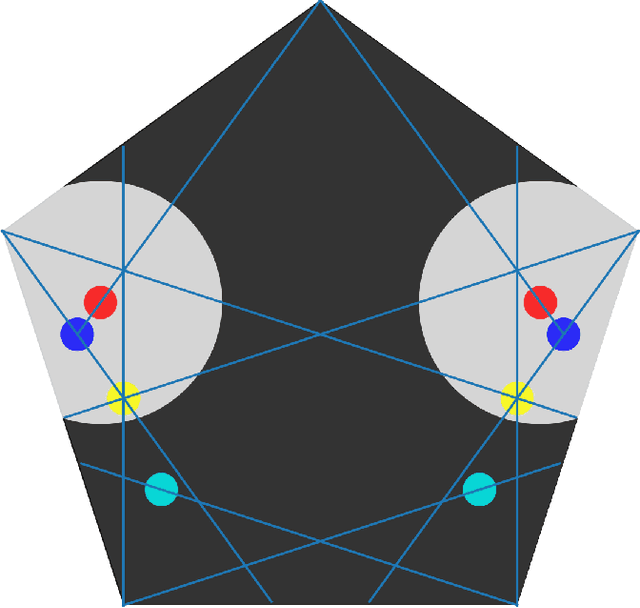
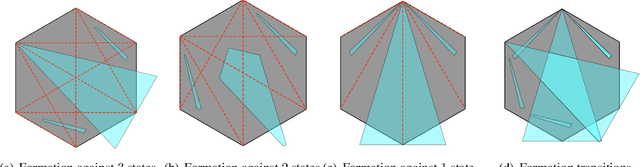
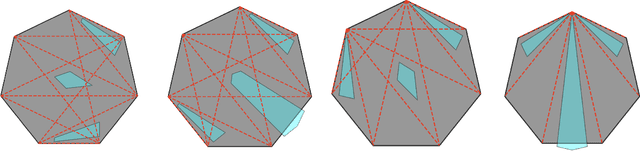
We study a pursuit-evasion problem which can be viewed as an extension of the keep-away game. In the game, pursuer(s) will attempt to intersect or catch the evader, while the evader can visit a fixed set of locations, which we denote as the anchors. These anchors may or may not be stationary. When the velocity of the pursuers is limited and considered low compared to the evaders, we are interested in whether a winning strategy exists for the pursuers or the evaders, or the game will draw. When the anchors are stationary, we show an algorithm that can help answer the above question. The primary motivation for this study is to explore the boundaries between kinematic and dynamic constraints. In particular, whether the solution of the kinematic problem can be used to speed up the search for the problems with dynamic constraints and how to discretize the problem to utilize such relations best. In this work, we show that a geometric branch-and-bound type of approach can be used to solve the stationary anchor problem, and the approach and the solution can be extended to solve the dynamic problem where the pursuers have dynamic constraints, including velocity and acceleration bounds.

Finding Control Synthesis for Kinematic Shortest Paths

This work presents the analysis of the properties of the shortest path control synthesis for the rigid body system. The systems we focus on in this work have only kinematic constraints. However, even for seemingly simple systems and constraints, the shortest paths for generic rigid body systems were only found recently, especially for 3D systems. Based on the Pontraygon's Maximum Principle (MPM) and Lagrange equations, we present the necessary conditions for optimal switches, which form the control synthesis boundaries. We formally show that the shortest path for nearby configurations will have similar adjoint functions and parameters, i.e., Lagrange multipliers. We further show that the gradients of the necessary condition equation can be used to verify whether a configuration is inside a control synthesis region or on the boundary. We present a procedure to find the shortest kinematic paths and control synthesis, using the gradients of the control constraints. Given the shortest path and the corresponding control sequences, the optimal control sequence for nearby configurations can be derived if and only if they belong to the same control synthesis region. The proposed procedure can work for both 2D and 3D rigid body systems. We use a 2D Dubins vehicle system to verify the correctness of the proposed approach. More verifications and experiments will be presented in the extensions of this work.

Towards Constructing Finer then Homotopy Path Classes

This work presents a new path classification criterion to distinguish paths geometrically and topologically from the workspace, which is divided through cell decomposition, generating a medial-axis-like skeleton structure. We use this information as well as the topology of the robot to bound and classify different paths in the configuration space. We show that the path class found by the proposed method is equivalent to and finer than the path class defined by the homotopy of paths. The proposed path classes are easy to compute, compare, and can be used for various planning purposes. The classification builds heavily upon the topology of the robot and the geometry of the workspace, leading to an alternative fiber-bundle-based description of the configuration space. We introduce a planning framework to overcome obstacles and narrow passages using the proposed path classification method and the resulting path classes.

Piecewise linear regressions for approximating distance metrics

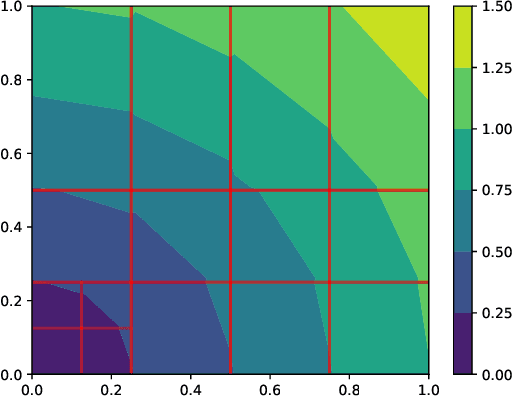
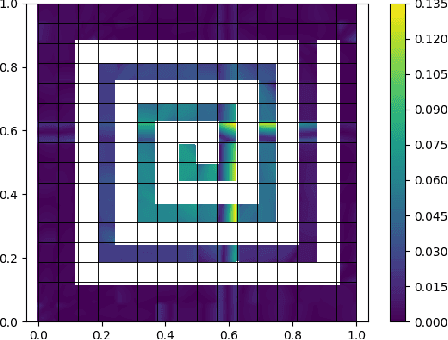
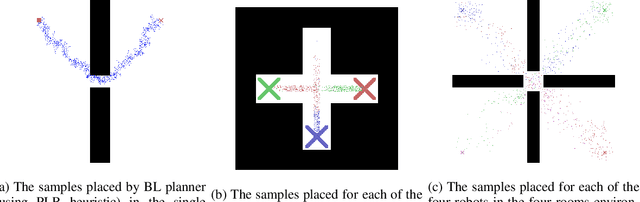
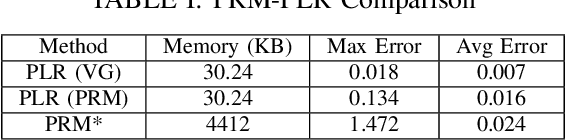
This paper presents a data structure that summarizes distances between configurations across a robot configuration space, using a binary space partition whose cells contain parameters used for a locally linear approximation of the distance function. Querying the data structure is extremely fast, particularly when compared to the graph search required for querying Probabilistic Roadmaps, and memory requirements are promising. The paper explores the use of the data structure constructed for a single robot to provide a heuristic for challenging multi-robot motion planning problems. Potential applications also include the use of remote computation to analyze the space of robot motions, which then might be transmitted on-demand to robots with fewer computational resources.

PuzzleFlex: kinematic motion of chains with loose joints

This paper presents a method of computing free motions of a planar assembly of rigid bodies connected by loose joints. Joints are modeled using local distance constraints, which are then linearized with respect to configuration space velocities, yielding a linear programming formulation that allows analysis of systems with thousands of rigid bodies. Potential applications include analysis of collections of modular robots, structural stability perturbation analysis, tolerance analysis for mechanical systems,and formation control of mobile robots.