Planning and Formulations in Pursuit-Evasion: Keep-away Games and Their Strategies
Paper and Code
Jun 16, 2022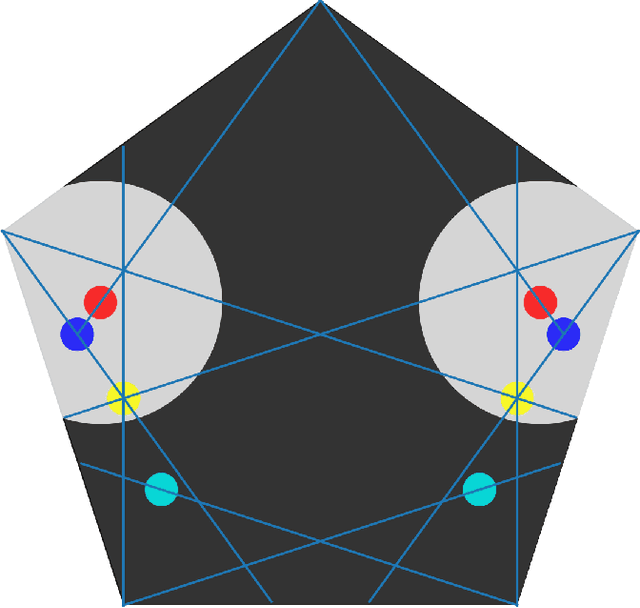

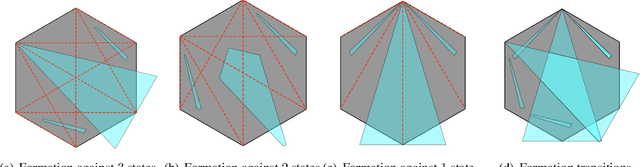
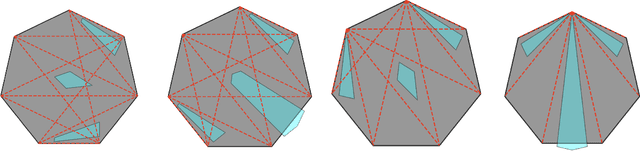
We study a pursuit-evasion problem which can be viewed as an extension of the keep-away game. In the game, pursuer(s) will attempt to intersect or catch the evader, while the evader can visit a fixed set of locations, which we denote as the anchors. These anchors may or may not be stationary. When the velocity of the pursuers is limited and considered low compared to the evaders, we are interested in whether a winning strategy exists for the pursuers or the evaders, or the game will draw. When the anchors are stationary, we show an algorithm that can help answer the above question. The primary motivation for this study is to explore the boundaries between kinematic and dynamic constraints. In particular, whether the solution of the kinematic problem can be used to speed up the search for the problems with dynamic constraints and how to discretize the problem to utilize such relations best. In this work, we show that a geometric branch-and-bound type of approach can be used to solve the stationary anchor problem, and the approach and the solution can be extended to solve the dynamic problem where the pursuers have dynamic constraints, including velocity and acceleration bounds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge